The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in x and CD in Y. Show that ar (AXYX)=12(ar||gm ABCD)
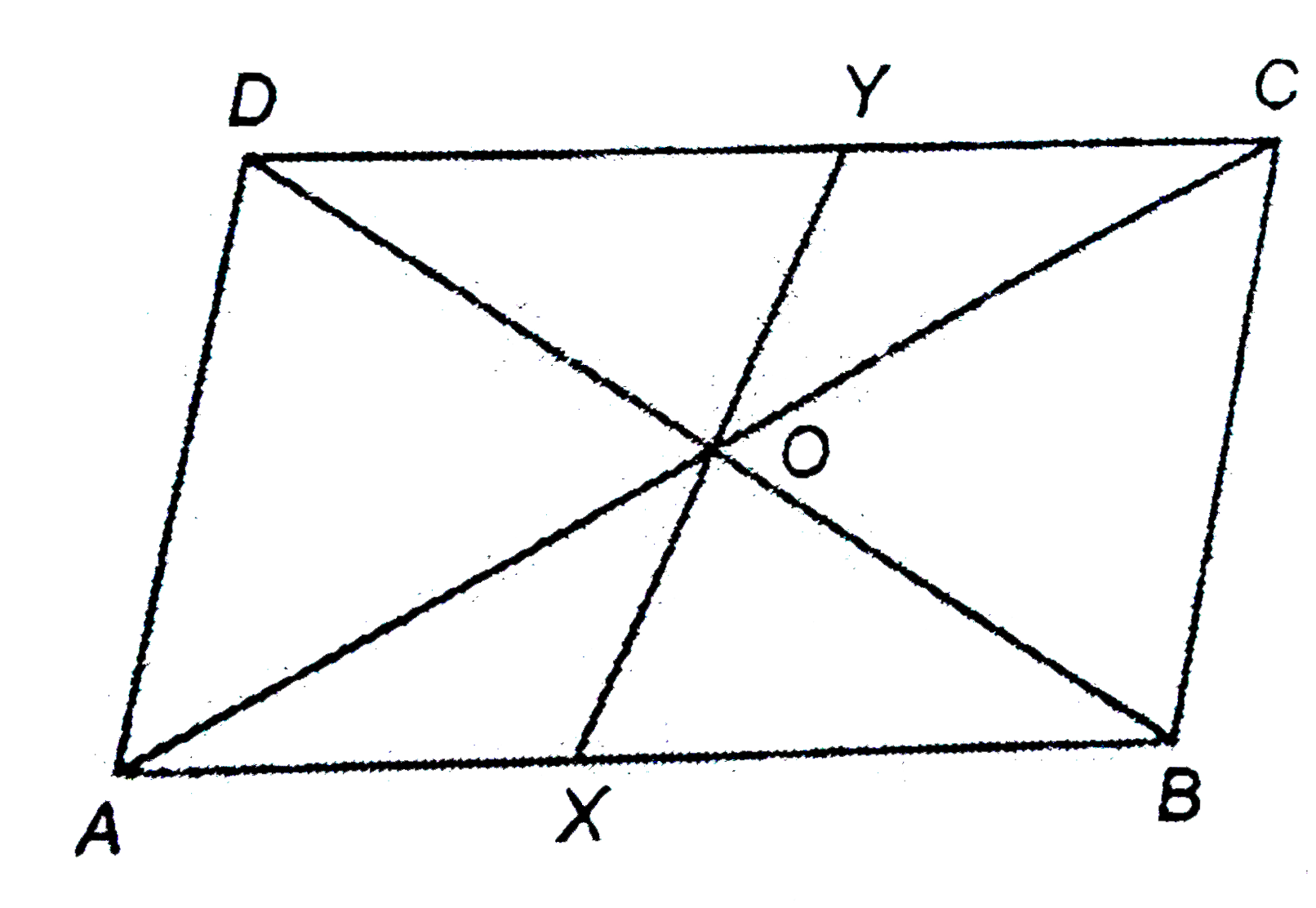
We know that, a diagonal of a parallelogram divides it into two triangles of equal areas.
Now, AC is the diagonal of parallelogram ABCD
∴ area of ΔACD=12× are of □ABCD...(1)
In ΔAOXandΔCOY,
.:⎧⎪⎨⎪⎩AO=CO∠AOX=∠COY∠OAX=∠OCY
∴ΔAOX≅ΔCOY
⇒ area of ΔAOX= area of ΔCOY
Now, area of ΔACD= are of □AOYD+ area of ΔOCY
− area of □AOYD+ area of ΔAOX [from (2)]
= area of □AXYD
∴ From (1), we get
area of □AXYD=12× area of □ABCD
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in X and CD in Y. Show that ar(AXYD)=12(ARgmABCD)
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=90∘ and ∠BDC=50∘, then ∠OAB= 40∘ (b) 50∘ (c) 10∘ (d) 900
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View Solution
