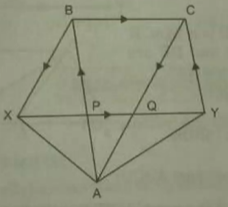
ABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
Given: ABCD is a trapezium with AB∥DC and XY∥AC.
Join YA, XC and XD.
△ACX and △ACY have same base AC and are between same parallels AC and XY.
So, ar(△ACX)=ar(△ACY) ......(i)
△ACX and △ADX have same base AX and are between same parallels AB and DC.
So, ar(△ACX)=ar(△ADX) ......(ii)
From (i) and (ii), we get
ar(△ADX)=ar(△ACY)
Hence Proved.
Topper's Solved these Questions
Similar Questions
ABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionABCD is a trapezium with AB ∣∣ DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC

View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC.AE intersects CD at F. Prove that ar ( ADF)= ar ( ECF) If the area of DFB=3 cm2, find the area of ^(gm) ABCD
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)
View Solution
