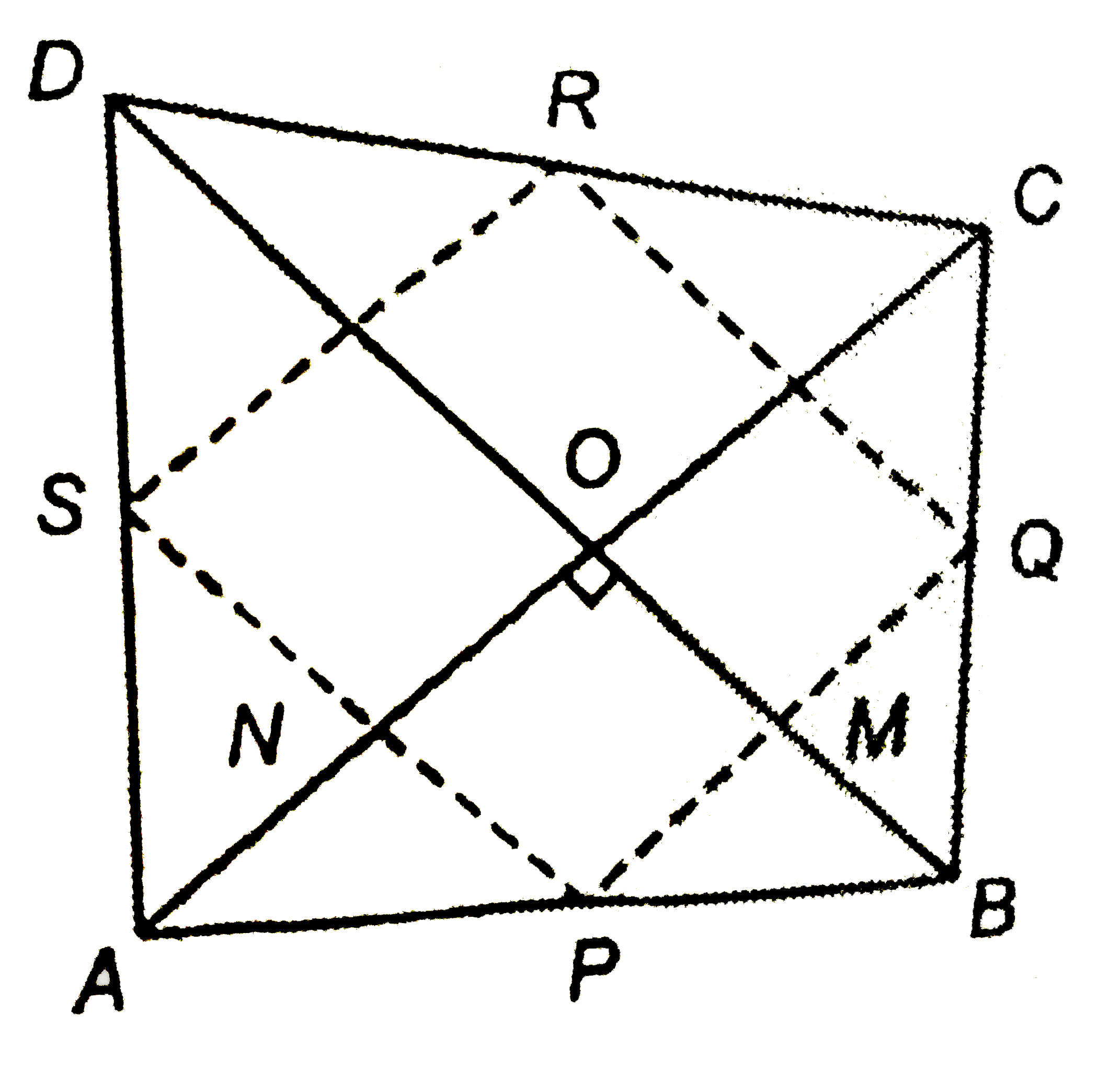
The diagonals of a quadrilateral are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
To show that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD, where the diagonals are perpendicular, is a rectangle, we can follow these steps:
Step 1: Identify the midpoints
Let the midpoints of sides AB, BC, CD, and DA be denoted as P, Q, R, and S respectively.
Step 2: Use the Midpoint Theorem
According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
- In triangle ABD, since P and S are midpoints of AB and AD, respectively, we have:
PS∥BDandPS=12BD
- In triangle BCD, since Q and R are midpoints of BC and CD, respectively, we have:
QR∥BDandQR=12BD
Step 3: Establish relationships between sides
From the above, we can conclude:
PS=QR
Step 4: Analyze triangles ABC and ADC
Now, consider triangles ABC and ADC.
- In triangle ABC, since P and Q are midpoints of AB and BC, respectively, we have:
PQ∥ACandPQ=12AC
- In triangle ADC, since S and R are midpoints of AD and CD, respectively, we have:
SR∥ACandSR=12AC
Step 5: Establish relationships between the other sides
From the above, we can conclude:
PQ=SR
Step 6: Conclude that opposite sides are equal
Now we have established:
- PS=QR
- PQ=SR
This means that opposite sides of quadrilateral PQRS are equal.
Step 7: Show that angles are right angles
Since the diagonals of quadrilateral ABCD are perpendicular, we can conclude that:
- Angles at the intersection point of the diagonals (let's denote it as O) are 90 degrees.
Using properties of parallel lines, we can show that:
- Angles P, Q, R, and S in quadrilateral PQRS are all 90 degrees because they are alternate interior angles formed by the transversal lines through the midpoints.
Step 8: Conclusion
Since we have established that:
- Opposite sides of quadrilateral PQRS are equal (PS=QR and PQ=SR)
- All angles in quadrilateral PQRS are 90 degrees
We can conclude that quadrilateral PQRS is a rectangle.
Let the midpoints of sides AB, BC, CD, and DA be denoted as P, Q, R, and S respectively.
According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
PS∥BDandPS=12BD
QR∥BDandQR=12BD
From the above, we can conclude:
PS=QR
Now, consider triangles ABC and ADC.
PQ∥ACandPQ=12AC
SR∥ACandSR=12AC
From the above, we can conclude:
PQ=SR
Now we have established:
- PS=QR
- PQ=SR
Since the diagonals of quadrilateral ABCD are perpendicular, we can conclude that:
- Angles at the intersection point of the diagonals (let's denote it as O) are 90 degrees.
- Angles P, Q, R, and S in quadrilateral PQRS are all 90 degrees because they are alternate interior angles formed by the transversal lines through the midpoints.
Since we have established that:
- Opposite sides of quadrilateral PQRS are equal (PS=QR and PQ=SR)
- All angles in quadrilateral PQRS are 90 degrees
Topper's Solved these Questions
Similar Questions
Show that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
 View Solution
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View Solution(−2,4),(4,8),(10,7) and (11,−5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
View SolutionProve that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
View Solution

