In ΔABC the lines are drawn parallel to BC,CA and AB respectively through A,B and C intersecting at P, Q and R. Find the ration of perimeter of ΔPQR and ΔABC
To find the ratio of the perimeter of triangle PQR to the perimeter of triangle ABC, we can follow these steps:
Step 1: Understand the Configuration
In triangle ABC, lines are drawn parallel to sides BC, CA, and AB through points A, B, and C respectively. These lines intersect at points P, Q, and R.
Hint: Visualize the triangles and the parallel lines to understand the relationships between the sides.
Step 2: Identify Parallelograms
The lines drawn create three parallelograms:
1. ABQP
2. BCRQ
3. CAPR
Hint: Remember that in a parallelogram, opposite sides are equal and parallel.
Step 3: Establish Relationships
From the properties of the parallelograms:
- BC=AQ and BC=AR (opposite sides of parallelogram ABQP)
- Therefore, AQ=AR, indicating that A is the midpoint of QR.
Similarly, we can establish:
- CA=PR and CA=PQ (from parallelogram CAPR)
- BQ=RP and BQ=QR (from parallelogram BCRQ)
Hint: Use the midpoint theorem to relate the sides of triangles ABC and PQR.
Step 4: Express Side Lengths
From the relationships established:
- AB=12PQ
- BC=12QR
- CA=12RP
Hint: This means each side of triangle ABC is twice the corresponding side of triangle PQR.
Step 5: Calculate the Perimeters
The perimeter of triangle ABC:
Perimeter of ABC=AB+BC+CA
The perimeter of triangle PQR:
Perimeter of PQR=PQ+QR+RP
Using the relationships:
PQ=2AB,QR=2BC,RP=2CA
Thus, the perimeter of triangle PQR:
Perimeter of PQR=2(AB+BC+CA)=2×Perimeter of ABC
Step 6: Find the Ratio
The ratio of the perimeter of triangle PQR to the perimeter of triangle ABC is:
Perimeter of PQRPerimeter of ABC=2×Perimeter of ABCPerimeter of ABC=2:1
Final Answer
The ratio of the perimeter of triangle PQR to the perimeter of triangle ABC is 2:1.
---
In triangle ABC, lines are drawn parallel to sides BC, CA, and AB through points A, B, and C respectively. These lines intersect at points P, Q, and R.
The lines drawn create three parallelograms:
1. ABQP
2. BCRQ
3. CAPR
From the properties of the parallelograms:
- BC=AQ and BC=AR (opposite sides of parallelogram ABQP)
- Therefore, AQ=AR, indicating that A is the midpoint of QR.
- CA=PR and CA=PQ (from parallelogram CAPR)
- BQ=RP and BQ=QR (from parallelogram BCRQ)
From the relationships established:
- AB=12PQ
- BC=12QR
- CA=12RP
The perimeter of triangle ABC:
Perimeter of ABC=AB+BC+CA
Perimeter of PQR=PQ+QR+RP
PQ=2AB,QR=2BC,RP=2CA
Perimeter of PQR=2(AB+BC+CA)=2×Perimeter of ABC
The ratio of the perimeter of triangle PQR to the perimeter of triangle ABC is:
Perimeter of PQRPerimeter of ABC=2×Perimeter of ABCPerimeter of ABC=2:1
The ratio of the perimeter of triangle PQR to the perimeter of triangle ABC is 2:1.
Topper's Solved these Questions
Similar Questions
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. Δ is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If perimeters of ΔLMNandΔABCanλandμ, then the value of λμ is
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionIn a ΔABC,D,EandF are the mid-point of sides BC, CA and AB respectively. If area of ΔABC=16cm2, find the area of trapezium FBCE
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
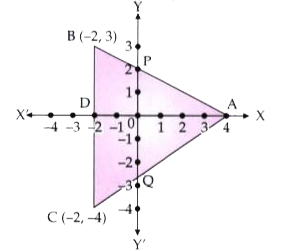
(iv) Find the equation of the line AC.
View SolutionPoints A, B, C lie on the parabola y2=4ax The tangents to the parabola at A, B and C, taken in pair, intersect at points P, Q and R. Determine the ratio of the areas of the △ABC and △PQR
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
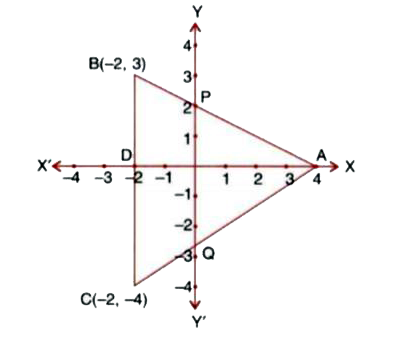
Find the length of AB and AC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
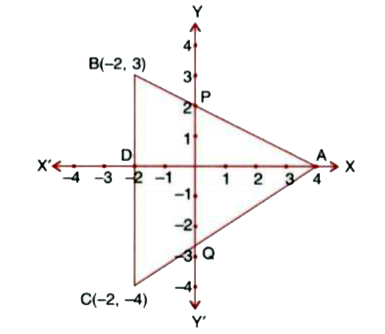
Write the co-ordinates of A.
View SolutionM and N divide the side AB of a triangle ABC into three equal parts . Through M and N, lines are drawn parallel to BC and intersecting AC at points P and Q respectively. Prove that P and Q divide AC into three equal parts.
View Solution
