The diagonals of a quadrilateral ABCD are equal. Prove that the quardilateral formed by joining the midpoints of its sides is a rhombus.
To prove that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD (where the diagonals AC and BD are equal) is a rhombus, we will follow these steps:
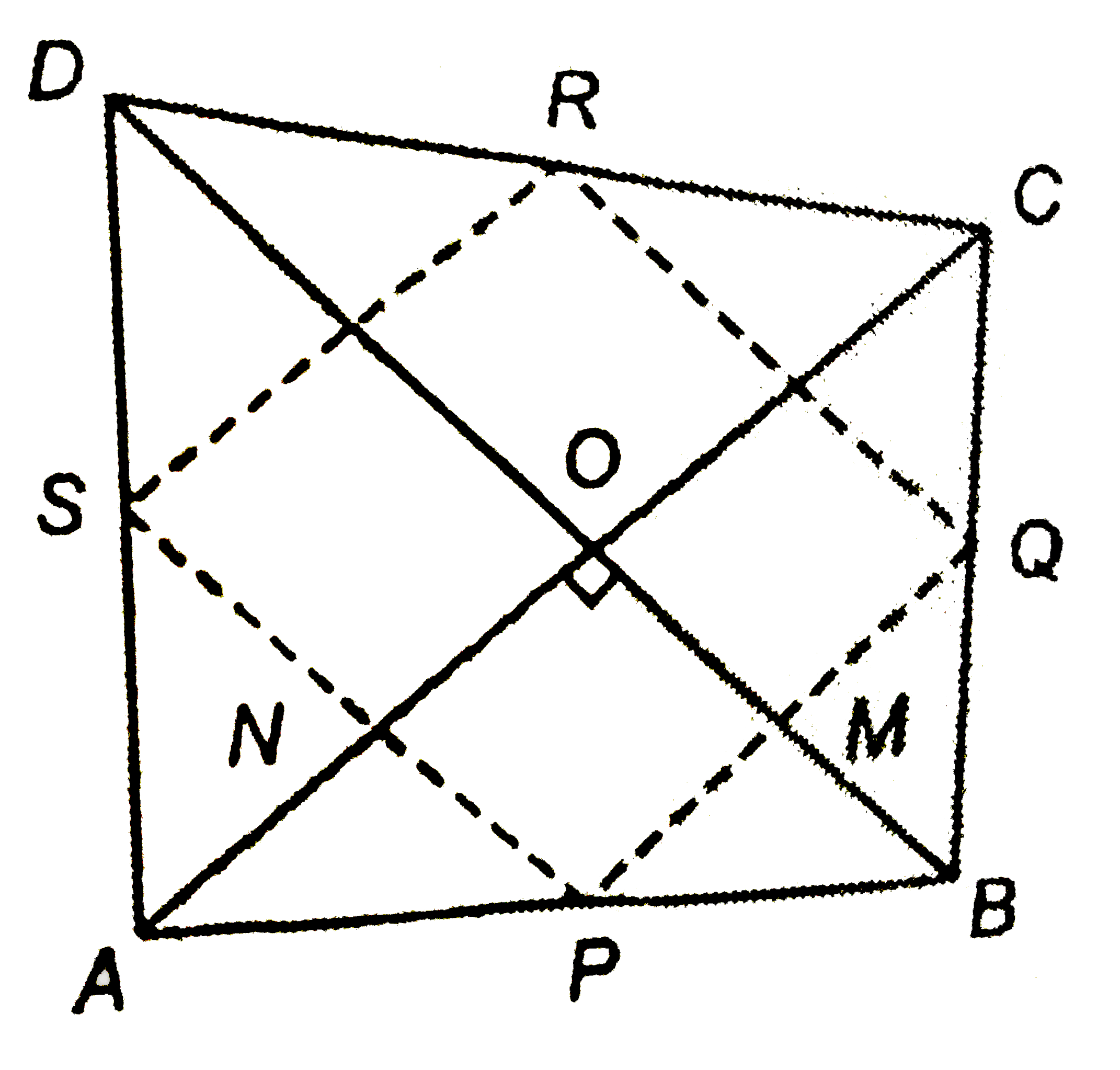
1. Draw Quadrilateral ABCD:
- Start by sketching quadrilateral ABCD with diagonals AC and BD intersecting at point O.
- Label the midpoints of sides AB, BC, CD, and DA as P, Q, R, and S respectively.
2. Identify Midpoints:
- Let P be the midpoint of AB, Q be the midpoint of BC, R be the midpoint of CD, and S be the midpoint of DA.
3. Apply the Midpoint Theorem:
- According to the midpoint theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
- In triangle ABC:
- Since P and Q are midpoints, PQ is parallel to AC and PQ = 1/2 * AC.
4. Consider Triangle BCD:
- In triangle BCD:
- Q and R are midpoints, so QR is parallel to BD and QR = 1/2 * BD.
5. Consider Triangle ACD:
- In triangle ACD:
- S and R are midpoints, so SR is parallel to AC and SR = 1/2 * AC.
6. Consider Triangle ABD:
- In triangle ABD:
- P and S are midpoints, so PS is parallel to BD and PS = 1/2 * BD.
7. Establish Parallel Sides:
- From the above steps, we have:
- PQ || RS (since both are parallel to AC)
- QR || PS (since both are parallel to BD)
8. Show Opposite Sides are Equal:
- Since AC = BD (given), we can conclude:
- PQ = 1/2 * AC and SR = 1/2 * AC, thus PQ = SR.
- QR = 1/2 * BD and PS = 1/2 * BD, thus QR = PS.
9. Conclude that Opposite Sides are Equal:
- We have established that:
- PQ = SR and QR = PS.
- Therefore, opposite sides of quadrilateral PQRS are equal.
10. Conclude that PQRS is a Rhombus:
- Since opposite sides are equal and parallel, quadrilateral PQRS is a rhombus.
Final Conclusion:
Thus, we have proved that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD is a rhombus.
---
- Start by sketching quadrilateral ABCD with diagonals AC and BD intersecting at point O.
- Label the midpoints of sides AB, BC, CD, and DA as P, Q, R, and S respectively.
- Let P be the midpoint of AB, Q be the midpoint of BC, R be the midpoint of CD, and S be the midpoint of DA.
- According to the midpoint theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
- In triangle ABC:
- Since P and Q are midpoints, PQ is parallel to AC and PQ = 1/2 * AC.
4. Consider Triangle BCD:
- In triangle BCD:
- Q and R are midpoints, so QR is parallel to BD and QR = 1/2 * BD.
- In triangle ACD:
- S and R are midpoints, so SR is parallel to AC and SR = 1/2 * AC.
- In triangle ABD:
- P and S are midpoints, so PS is parallel to BD and PS = 1/2 * BD.
- From the above steps, we have:
- PQ || RS (since both are parallel to AC)
- QR || PS (since both are parallel to BD)
- Since AC = BD (given), we can conclude:
- PQ = 1/2 * AC and SR = 1/2 * AC, thus PQ = SR.
- QR = 1/2 * BD and PS = 1/2 * BD, thus QR = PS.
- We have established that:
- PQ = SR and QR = PS.
- Therefore, opposite sides of quadrilateral PQRS are equal.
- Since opposite sides are equal and parallel, quadrilateral PQRS is a rhombus.
Thus, we have proved that the quadrilateral formed by joining the midpoints of the sides of quadrilateral ABCD is a rhombus.
Similar Questions
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View Solutionprove using vectors: The quadrilateral obtained by joining mid-points of adjacent sides a rectangle is a rhombus.
View SolutionIf the opposite sides of a quadrilateral are equal, prove that the quadrilateral is a parallelogram.
View SolutionIf the diagonals of a quadrilateral bisect each other at right angle, prove that the quadrilateral is a rhombus.
View SolutionProve using vectors: The quadrilateral obtained by joining mid points of adjacent sides of a rectangle is a rhombus.
View SolutionConsider the - following statements in respect of a quadrilateral :
1. The line segments joining the midpoints of the two pairs of opposite sides bisect each other at the point of intersection.
2. The area of the quadrilateral formed by joining the midpoints of the four adjacent sides is half of the total area of the quadrilateral.
Which of the statements given above is/are correct ?
View Solution
