The diagonals of the square ABCD intersect each other at O .Let OP⊥AB is constructed. Prove that ∠AOP=∠PBO Solution in Bengali
Step by step video & image solution for The diagonals of the square ABCD intersect each other at O .Let OPbotAB is constructed. Prove that angleAOP =anglePBO by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF PARALLELOGRAMBOOK - CALCUTTA BOOK HOUSECHAPTER - PROPERTIES OF PARALLELOGRAMEXERCISE - EXERCISE - 1 (Short -answer type questions )
10 Videos
- PROBABILITYBOOK - CALCUTTA BOOK HOUSECHAPTER - PROBABILITYEXERCISE - EXERCISE - 2
16 Videos
- REAL NUMBERS BOOK - CALCUTTA BOOK HOUSECHAPTER - REAL NUMBERS EXERCISE - Exercise 1.4 ( Long answer)
18 Videos
Similar Questions
Find the angles of the parallelogram ABCD , if ∠C:∠D=4:5
View SolutionDefine with examples :
Event.
View SolutionIf E be a random experiment or rolling a dice and S be its sample space, then if one dice is rolled then find the sample space of it and also find the probability of not getting 4.
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solutionचतुर्भुज ABCD के विकर्ण एक -दूसरे को बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि AOBO=CODO तो सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है ।

View SolutionThe diagonals of the quadrilateral ABCD intersect each other at O in such a way that AOBO=CODO. Prove that ABCD is a trapezium.
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO show that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
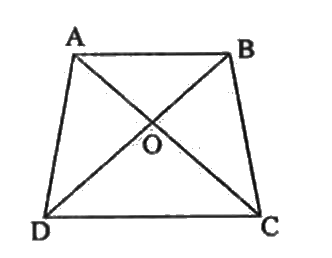
View SolutionIn the trapezium ABCD, AB || DC. The diagonals AC and BD of it intersects each other at O. Prove that ΔAOD=ΔBOC.
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersects each other at O such that ΔAOD=ΔBOC. Prove that ABCD is trapezium.
View SolutionIn the parallelogram ABCD, the midpoints of BC and AD are Q and P respectively. If the diagonals of the parallelogram ABCD intersect each other at point O, prove that POQ will be a straight line.
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at point ‘O’ such that AOBO=CODO. Prove that ABCD is a trapezium
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at point ‘O’ such that AOBO=CODO. Prove that ABCD is a trapezium
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View Solution
