E and F are the mid - points of AB and AC respectively of ΔABC . The st. line EF is extended to the point D such that EF = FD. Prove that ADCE is a parallelogram.Solution in Bengali
Step by step video & image solution for E and F are the mid - points of AB and AC respectively of DeltaABC . The st. line EF is extended to the point D such that EF = FD. Prove that ADCE is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF PARALLELOGRAMBOOK - CALCUTTA BOOK HOUSECHAPTER - PROPERTIES OF PARALLELOGRAMEXERCISE - EXERCISE - 1 (Short -answer type questions )
10 Videos
- PROBABILITYBOOK - CALCUTTA BOOK HOUSECHAPTER - PROBABILITYEXERCISE - EXERCISE - 2
16 Videos
- REAL NUMBERS BOOK - CALCUTTA BOOK HOUSECHAPTER - REAL NUMBERS EXERCISE - Exercise 1.4 ( Long answer)
18 Videos
Similar Questions
Find the angles of the parallelogram ABCD , if ∠C:∠D=4:5
View SolutionDefine with examples :
Event.
View SolutionIf E be a random experiment or rolling a dice and S be its sample space, then if one dice is rolled then find the sample space of it and also find the probability of not getting 4.
View SolutionLet ABC be a given isosceles triangle with AB=AC . Sides ABandAC are extended up to EandF, respectively, such that BExCF=AB2. Prove that the line EF always passes through a fixed point.
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View Solutionयदि ΔABCकी भुजाओं BC,CA और AB के मध्यबिंदु क्रमशः D,E और F हों तो सिद्ध कीजिए कि AD रेखाखंड EF को समद्विभाजित करती है।
View SolutionIf the mid-points of AB, BC and CA of the ΔABC are D, E and F respectively, P and Q are also the mid-points of DE and EF respectively. Then PQ =
View SolutionOne card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a spade.
View SolutionABCD is a trapezium in which AB || DC and E is the mid-point of AD. If F be a point on BC such that EF || DC, then prove that EF=12(AB+DC).
View SolutionLet ABC be a given right isosceles triangle withAB=AC. Sides AB and AC are extended up to E and F, respectively, such that BE×CF=AB2 . Prove that the line EF always passes through a fixed point.
View SolutionIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
View SolutionIn given Fig.
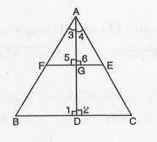 , ΔABC is isosceles with AB = AC. D, E, F are the mid-points of sides BC, AC and AB respectively. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
, ΔABC is isosceles with AB = AC. D, E, F are the mid-points of sides BC, AC and AB respectively. Show that the line segment AD is perpendicular to the line segment EF and is bisected by it.
View Solutionमाना कि ABC एक समद्विबाहु त्रिभुज हैं, जहाँ AB=AC तथा D,E तथा F क्रमशः BC,CA तथा AB के मध्य-बिंदु हैं, तो सिद्ध करें कि AD ⊥ EF तथा EF ,AD को समद्विभाजित करती है।
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH

View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
3DF=EF
View Solution
