The diagrams given below represent relations from X to Y. Classify them as relation or function. If the relation is a function, classify it as one - one or many - one.
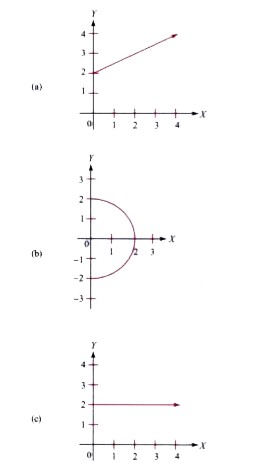
The correct Answer is:(a) Function, one -to-one
(b) Not one function
(c ) Function, many-to-one
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - TEST YOURSELF (Level 3)12videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - TEST YOURSELF (Level 3) (Multiple Choice Questions)29videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - TEST YOURSELF (Level 3) (Multiple Choice Questions)29videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RATIONAL EXPRESSIONSEXERCISE - Olympiad and ntse level exercises10videos
RATIONAL EXPRESSIONS
- BOOK - CENGAGECHAPTER - REMAINDER THEOREMEXERCISE - TEST YOURSELF (Multiple Choice Questions) OLYMPIAD AND NTSE LEVEL EXERCISES10videos
REMAINDER THEOREM
Similar Questions
Knowledge Check
- Question 1 - Select One
Which one is correct in the relation
Av=nλBλ=vnCn=vλDn=λT - Question 2 - Select One
Identify the diagram and related function
 ASimple cuboidal epithelium DiffusionBSimple Squamous epithelium Secretion and absorptionCCompound epithelium ProtectionDCompound epithelium Diffusion
ASimple cuboidal epithelium DiffusionBSimple Squamous epithelium Secretion and absorptionCCompound epithelium ProtectionDCompound epithelium Diffusion - Question 3 - Select One
Which one is related to immunity
APineal glandBThymusCAdrenal glandDParathyroid gland.
A function f given as f:{(2,7),(3,4),(7,9),(−1,6),(0,2),(5,3)}. Is this function one-one onto?
Interchange the order of the elements in the ordered pairs and form the new relation. Is this relation a function? If it is a function, is it one-one onto.View SolutionClassify the following functions in the form of one-one, many one, into and onto, also give reason to support your answer.
View SolutionDoes the following graph represent a function or a relation?
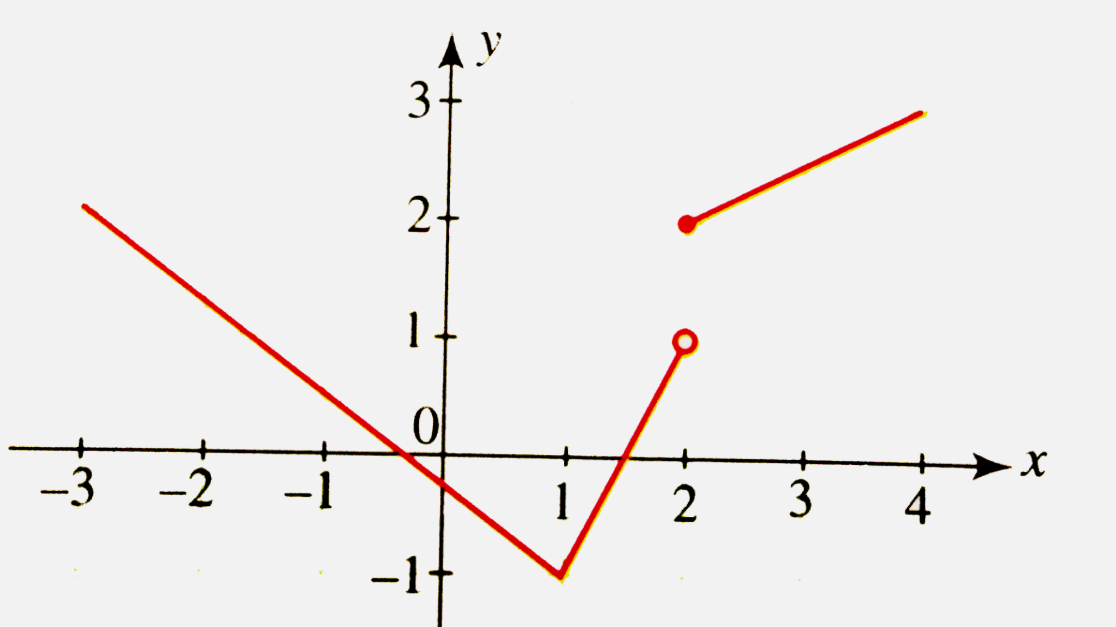 View Solution
View SolutionDoes the following graph represent a function or a relation?
 View Solution
View SolutionConsider the following statements in respect of relations and functions:
1. All relations are functions but all functions are not relations.
2. A relation from A to B is a subset of Cartesian product A x B.
3. A relation in A is a subset of Cartesian product A x A.
Which of the above statements are correct?View Solution

