The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as $(l_{1}, m_{1}, n_{1}), (l_{2}, m_{2}, n_{2}), (l_{3}, m_{3}, n_{3})$ are

A

$l_{1} + l_{2} + l_{3}, m_{1} + m_{2} + m_{3}, n_{1} + n_{2} + n_{3}$

B

$\frac{l_{1} + l_{2} + l_{3}}{\sqrt{3}}, \frac{m_{1} + m_{2} + m_{3}}{\sqrt{3}}, \frac{n_{1} + n_{2} + n_{3}}{\sqrt{3}}$

C

$\frac{l_{1} + l_{2} + l_{3}}{3}, \frac{m_{1} + m_{2} + m_{3}}{3}, \frac{n_{1} + n_{2} + n_{3}}{3}$

D

none of these

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To find the direction cosines of a line that equally inclines to three mutually perpendicular lines, we can follow these steps:
Step 1: Understand the Direction Cosines
The direction cosines of a line are represented as $(l, m, n)$ . For three mutually perpendicular lines with direction cosines $(l_{1}, m_{1}, n_{1})$ , $(l_{2}, m_{2}, n_{2})$ , and $(l_{3}, m_{3}, n_{3})$ , we know that the following conditions hold:
1. $l_{1}^{2} + m_{1}^{2} + n_{1}^{2} = 1$
2. $l_{2}^{2} + m_{2}^{2} + n_{2}^{2} = 1$
3. $l_{3}^{2} + m_{3}^{2} + n_{3}^{2} = 1$
4. The dot products of the direction cosines of any two lines are zero:
- $l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0$
- $l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3} = 0$
- $l_{1} l_{3} + m_{1} m_{3} + n_{1} n_{3} = 0$
Step 2: Set Up the Equations
Since the line is equally inclined to the three mutually perpendicular lines, we can express the conditions mathematically. The line's direction cosines $(l, m, n)$ must satisfy:
- $l = m = n$
Step 3: Use the Condition of Equally Inclined
Since the line is equally inclined to the three lines, we can use the fact that the direction cosines can be expressed as:
$l^{2} + m^{2} + n^{2} = 1$
Substituting $l = m = n$ gives:
$3 l^{2} = 1 ⟹ l^{2} = \frac{1}{3} ⟹ l = \pm \frac{1}{\sqrt{3}}$
Thus, we have:
$l = m = n = \frac{1}{\sqrt{3}} or - \frac{1}{\sqrt{3}}$
Step 4: Conclusion
The direction cosines of the line that equally inclines to the three mutually perpendicular lines are:
$(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}) or (- \frac{1}{\sqrt{3}}, - \frac{1}{\sqrt{3}}, - \frac{1}{\sqrt{3}})$

|

Updated on:7/8/2024

Class 12 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as $(l_{1}, m_{1}, n_{1}), (l_{2}, m_{2}, n_{2}), (l_{3}, m_{3}, n_{3})$ are
Athe direction cosines of three mutually perpendicular lines
Bthe direction ratios of three mutually perpendicular lines which are not direction cosines.
Cthe direction cosines of three lines which need not be perpendicular
Dthe direction of three lines which need not be perpendicular
Question 2 - Select One
The direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as $l_{1}, m_{1}, n_{1}, l_{2}, m_{2}, n_{2}$ and $l_{3}, m_{3}, n_{3}$ are
A $l_{1} + l_{2} + l_{3}, m_{1} + m_{2} + m_{3}, n_{1} + n_{2} + n_{3}$
B $\frac{l_{1} + l_{2} + l_{3}}{\sqrt{3}}, \frac{m_{1} + m_{2} + m_{3}}{\sqrt{3}}, \frac{n_{1} + n_{2} + n_{3}}{\sqrt{3}}$
C $\frac{l_{1} + l_{2} + l_{3}}{3}, \frac{m_{1} + m_{2} + m_{3}}{3}, \frac{n_{1} + n_{2} + n_{3}}{3}$
Dnone of these
Question 3 - Select One
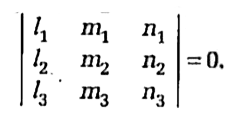
If $l_{1}, m_{1}, n_{1}, l_{2}, m_{2}, n_{2} and l_{3}, m_{3}, n_{3}$ are direction cosines of three mutuallyy perpendicular lines then, the value of $∣ ∣ ∣ ∣ \begin{matrix} l_{1} & m_{1} & n_{1} l_{2} & m_{2} & n_{2} l_{3} & m_{3} & n_{3} \end{matrix} ∣ ∣ ∣ ∣$ is
A $l_{3} m_{3} n_{3}$
B $\pm 1$
C $l_{1} m_{1} n_{1}$
D $l_{2} m_{2} n_{2}$

ML KHANNA-CO-ORDINATE GEOMETRY OF THREE DIMENSION-PROBLEM SET (3)

Home
Ask Doubt
Profile