The distance of point $A (- 2, 3, 1)$ from the line $P Q$ through $P (- 3, 5, 2),$ which makes equal angles with the axes is

A

$2 / \sqrt{3}$

B

$\sqrt{14 / 3}$

C

$16 / \sqrt{3}$

D

$5 / \sqrt{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Here, $α = β = γ$
$∵ {cos}^{2} α + {cos}^{2} β + {cos}^{2} γ = 1$
$∵ cos α = \frac{1}{\sqrt{3}}$
Direction cosines of PQ are $(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$

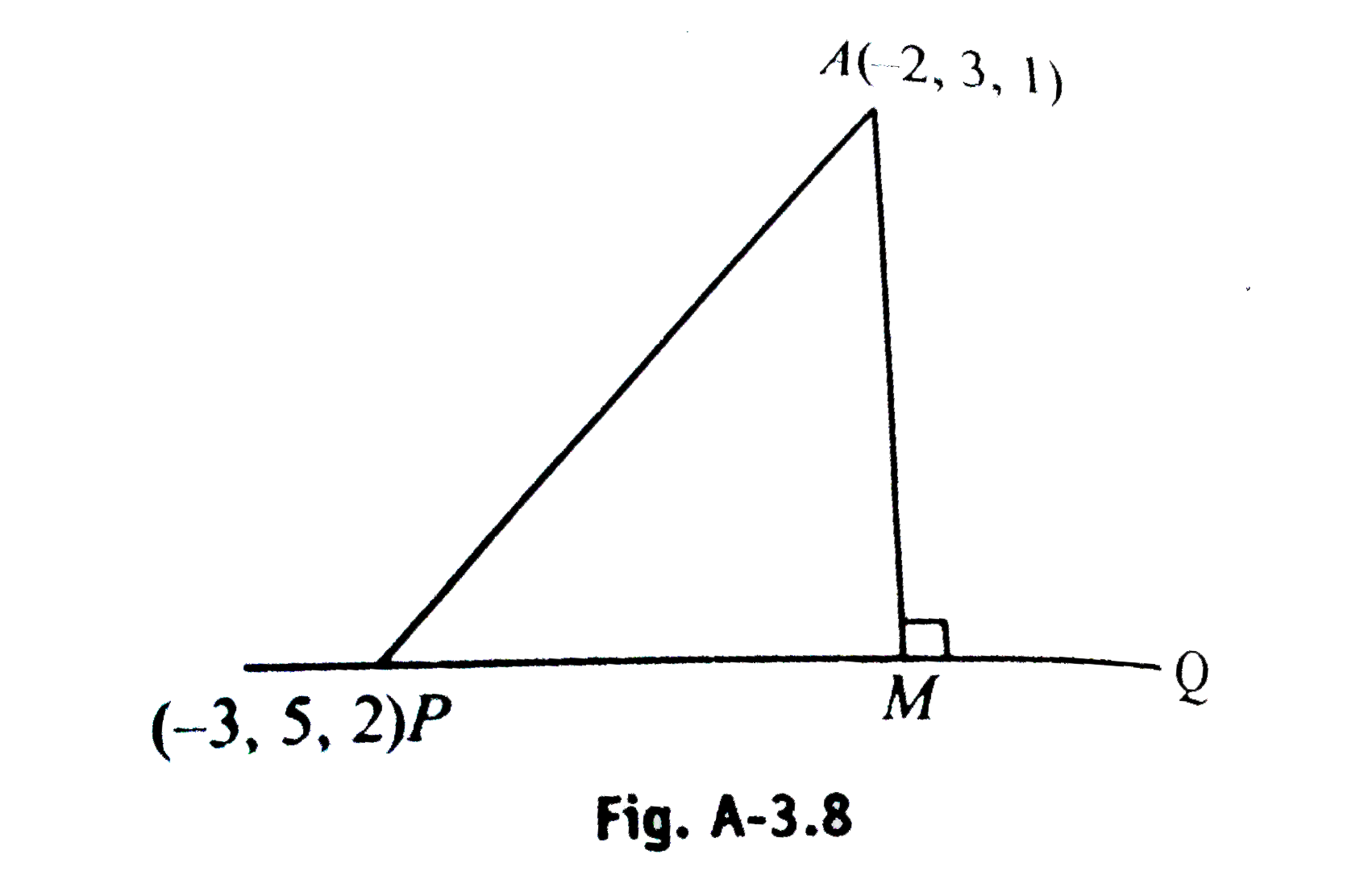
PM=Projection of AP on PQ
$= ∣ ∣ ∣ (- 2 + 3) \frac{1}{\sqrt{3}} + (3 - 5) \frac{1}{\sqrt{3}} + (1 - 2) \frac{1}{\sqrt{3}} ∣ ∣ ∣$
$= \frac{2}{\sqrt{3}}$
and $A P = \sqrt{{(- 2 + 3)}^{2} + {(3 - 5)}^{2} + {(1 - 2)}^{2}} = \sqrt{6}$
$A M = \sqrt{{(A P)}^{2} - {(P M)}^{2}} = \sqrt{6 - \frac{4}{3}} = \sqrt{\frac{14}{3}}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of the line through $(1, 2)$ , which makes equal intercepts on the axes is
A $x + y = 1$
B $x + y = 2$
C $x + y = 4$
Dnone of these
Question 2 - Select One
The distance of the point P(1,2,3) from the line which passes through the point (4,2,2) and parallel to the vector $2 ˆ i + 3 ˆ j + 6 ˆ k$ is
A $\sqrt{10}$
B $\sqrt{7}$
C $\sqrt{5}$
D1
Question 3 - Select One
A normal line with positive direction cosines to the plane P makes equal angles with the coordinate axis. The distance of the point A(1, 2, 3) from the line $\frac{x - 1}{1} = \frac{y + 2}{1} = \frac{z - 3}{2}$ measured parallel to the plane P is equal to
A3 units
B $\sqrt{13}$ units
C $\sqrt{14}$ units
D $2 \sqrt{5}$ units

CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise (Single)

Home
Ask Doubt
Profile