The distribution consists of three components with frequencies 45 , 40 and 15 having their means 2,2.5 and 2 respectively . The mean of the combined distribution is
220
2.2
100
45
The correct Answer is:B
To find the mean of the combined distribution, we can follow these steps:
Step 1: Identify the given data
We have three components with the following frequencies and means:
- Frequency f1=45, Mean x1=2
- Frequency f2=40, Mean x2=2.5
- Frequency f3=15, Mean x3=2
Step 2: Calculate the total frequency
The total frequency N is the sum of all individual frequencies:
N=f1+f2+f3=45+40+15=100
Step 3: Calculate the weighted sum of the means
To find the combined mean, we need to calculate the weighted sum of the means, which is given by:
Weighted Sum=(f1⋅x1)+(f2⋅x2)+(f3⋅x3)
Calculating each term:
- f1⋅x1=45⋅2=90
- f2⋅x2=40⋅2.5=100
- f3⋅x3=15⋅2=30
Now, summing these values:
Weighted Sum=90+100+30=220
Step 4: Calculate the combined mean
The combined mean ¯x is calculated using the formula:
¯x=Weighted SumN
Substituting the values we found:
¯x=220100=2.2
Conclusion
The mean of the combined distribution is 2.2.
---
We have three components with the following frequencies and means:
- Frequency f1=45, Mean x1=2
- Frequency f2=40, Mean x2=2.5
- Frequency f3=15, Mean x3=2
The total frequency N is the sum of all individual frequencies:
N=f1+f2+f3=45+40+15=100
To find the combined mean, we need to calculate the weighted sum of the means, which is given by:
Weighted Sum=(f1⋅x1)+(f2⋅x2)+(f3⋅x3)
Calculating each term:
- f1⋅x1=45⋅2=90
- f2⋅x2=40⋅2.5=100
- f3⋅x3=15⋅2=30
Weighted Sum=90+100+30=220
The combined mean ¯x is calculated using the formula:
¯x=Weighted SumN
Substituting the values we found:
¯x=220100=2.2
The mean of the combined distribution is 2.2.
Topper's Solved these Questions
- STATISTICS BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - STATISTICS EXERCISE - Exam Booster for Cracking Exam
25 Videos
- SOLVED PAPER 2019BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - SOLVED PAPER 2019EXERCISE - SECTION I: MATHEMATICS
48 Videos
- TAXATION BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TAXATION EXERCISE - EXAM BOOSTER
14 Videos
Similar Questions
Knowledge Check
A distribution consists of three components with frequencies 45, 40 and 15 having their means 2, 2.5 and 2, respectively. The mean of the combined. distribution is
A220B2.2C100D45(x + 2), x and (x - 1) are the frequencies of the numbers 12, 15 and 20 respectively. If the mean of the distribution is 14.5, the value of x is
A2B3C4D5The distributions X and Y with total number of observations 36 and 64 and means 4 and 3 respectively are combined. What is the mean of the resulting distribution X+Y?
A3.26B3.32C3.36D3.42
Find the mean of the following frequency distribution:

View SolutionFind the mean of the followings frequency distribution :

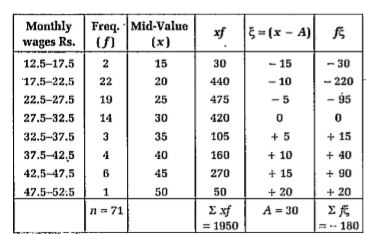
View SolutionCompute the mean (M) from the frequency distribution
View SolutionFind the mean for the following frequency distribution :
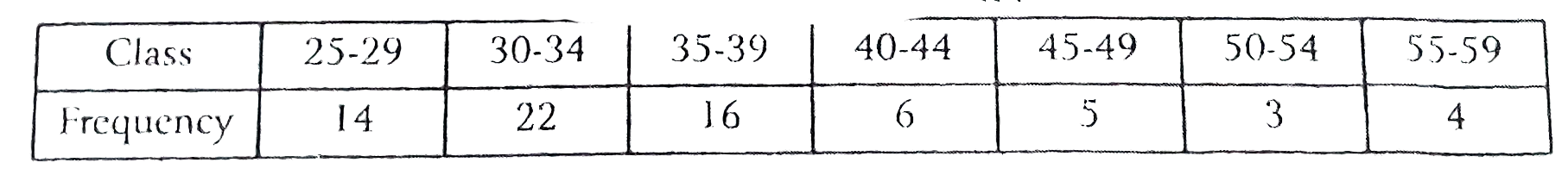
View SolutionThe distributions X and Y with total number of observations 36 and 64, and mean 4 and 3 respectively are combined. What is the mean of the resulting distribution X + Y?
View Solution


