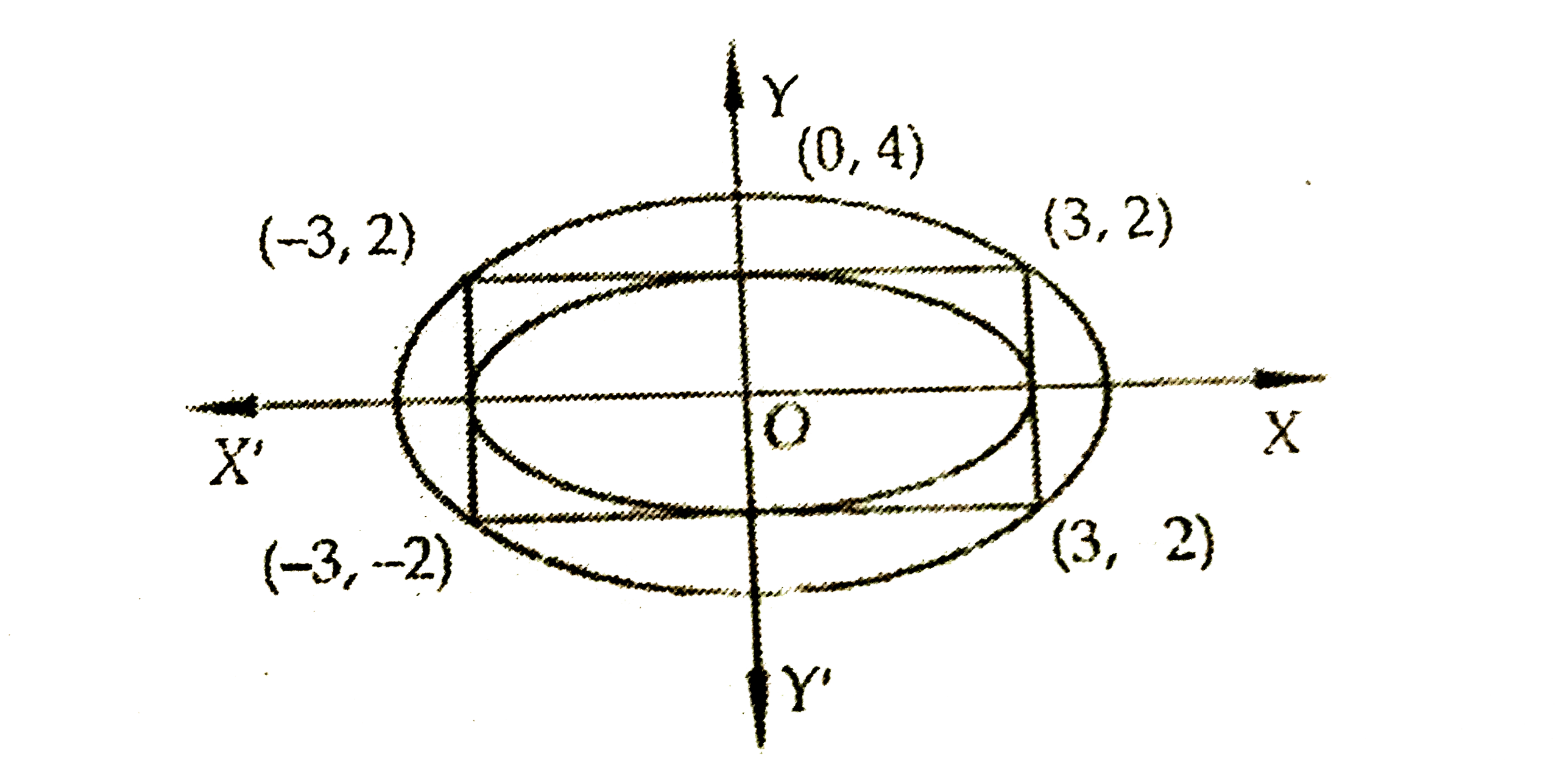
The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
√22
√32
12
34
The correct Answer is:C
Let the equation of the ellipse E2bex2a2+Y2b2=1.
it passes through (3,2) and (0,4)
∴9a2+4b2=1and16b2=1
⇒b=4anda2=12
let e be the eccentricity of ellipse E2 then ,
e=√1−a2b2=√1−1216=12
ALITER the equation of second degree curve passing through the intersection of x=3,x=−3,y=2andy=−2 is
(x+3)(x−3)+λ(y+2)(y−2)=0
it passes through (0,4)
∴−9+12λ=0⇒λ=34
 ltbrlt puting λ=34 in (i) we get 4x^(2)+3y^(2)=48 or ,(x^(2))/(12)+(y^(2))/(16)=1<br>≤tebeeentricity,thene=sqrt(1-(12)/(16))=(1)/(2)
ltbrlt puting λ=34 in (i) we get 4x^(2)+3y^(2)=48 or ,(x^(2))/(12)+(y^(2))/(16)=1<br>≤tebeeentricity,thene=sqrt(1-(12)/(16))=(1)/(2)
Topper's Solved these Questions
- ELLIPSEBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ELLIPSEEXERCISE - Section I - Solved Mcqs
59 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ELLIPSEEXERCISE - Section II - Assertion Reason Type
7 Videos
- DIFFERENTIATIONBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test
30 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
Similar Questions
The eccentricity of te ellipse x216+y24=1 is _______
View Solutionthe equation of the ellipse passing through (2,1) having e=1/2 , is
View SolutionThe eccentricity of ellipse 4(x−2y+1)2+9(2x+y+2)2=180 is
View SolutionThe eccentricity of the ellipse 4x2+9y2=36 is a.12√3 b. 1√3 c. √53 d. √56
View SolutionThe eccentricity of the ellipse 4x2+9y2=36 is
a.12√3
b. 1√3
c. √53
d. √56
View SolutionThe eccentricity of the ellipse, which passes through the points (2, −2) and (−3,1) is :
View SolutionThe eccentricity of the ellipse 4x2+9y2+8x+36y+4=0 is a.56 b. 35 c. √23 d. √53
View SolutionIf e' is the eccentricity of the ellipse x2a2+y2b2=1 (a>b), then
View SolutionThe eccentricity of the ellipse 5x2+9y2=1 is a.2/3 b. 3/4 c. 4/5 d. 1/2
View SolutionThe eccentricity of the ellipse 5x2+9y2=1 is a.2/3 b. 3/4 c. 4/5 d. 1/2
View Solution
