The equation of a circle is $x^{2} + y^{2} = 4 .$ Find the center of the smallest circle touching the circle and the line $x + y = 5 \sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(\frac{7}{2 \sqrt{2}}, \frac{7}{2 \sqrt{2}})$

Here, OB $=$ Radius $= 2$
The distance of (0,0) from $x + y = 5 \sqrt{2}$ is 5.
Therefore, the radius of the smallest circle is $(5 - 2) / 2 = 3 / 2,$ and $O C = 2 + 3 / 27 / 2$ .
The slope of OA is $1 = tan θ,$
Therefore,
$cos θ = \frac{1}{\sqrt{2}}, sin θ = \frac{1}{\sqrt{2}}$
$∴ C \equiv (0 + O C . cos θ, 0 + O C . sin θ) \equiv (\frac{7}{2 \sqrt{2}}, \frac{7}{2 \sqrt{2}})$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

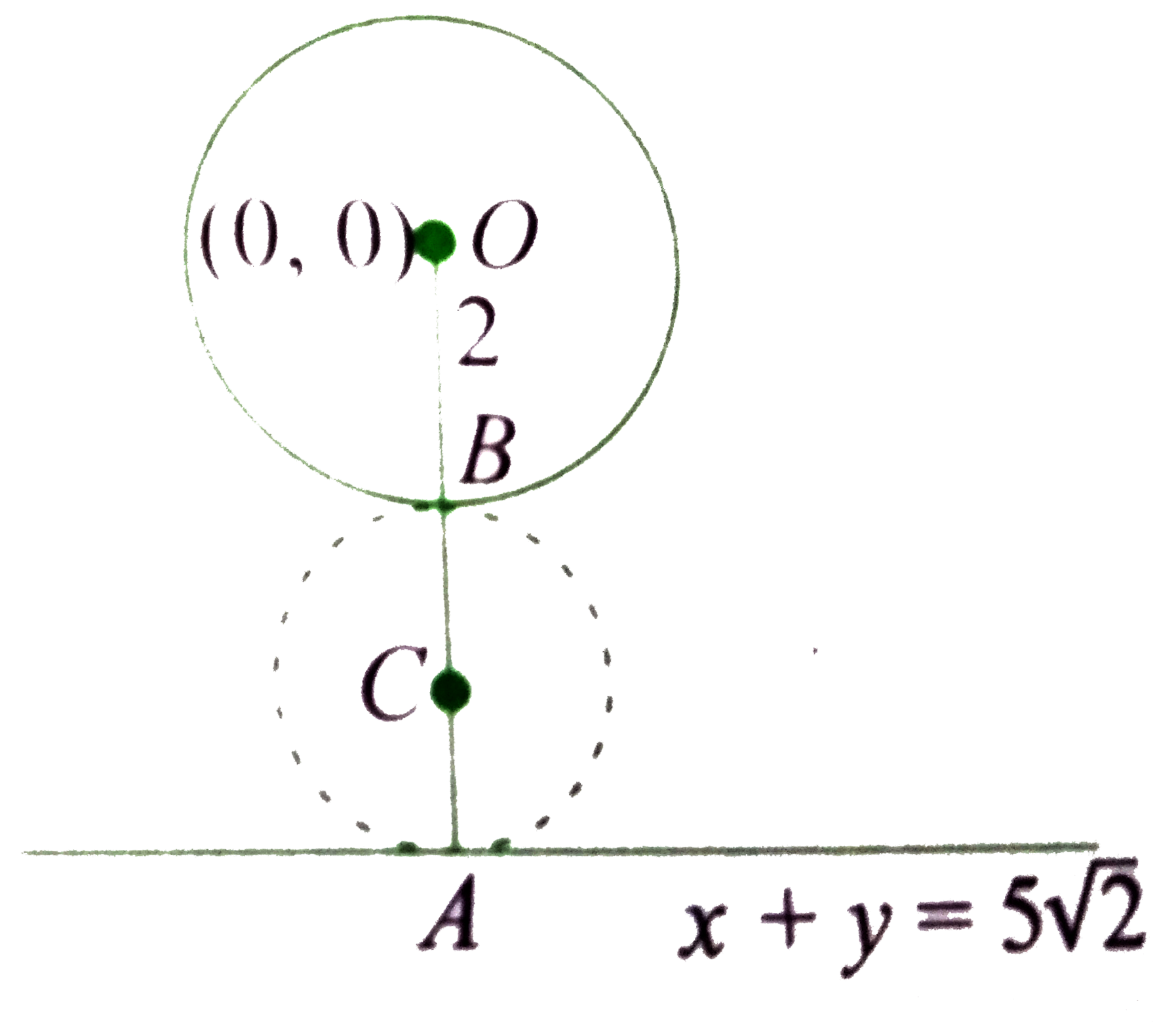
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of the circle touching the lines $| y |$ = x and having radius $\sqrt{2}$ is :
A $x^{2} + y^{2} + 4 x + 2 = 0$
B $x^{2} + y^{2} - 6 x + 7 = 0$
C $x^{2} + y^{2} - 4 x + 2 = 0$
D $x^{2} + y^{2} - 4 x - 3 = 0$

CENGAGE-CIRCLE -Exercise 4.5

Home
Ask Doubt
Profile