The equation of motion of a particle is
s=2t2+sin2t
, where
s
is in metres and
t
is in seconds. The velocity of the particle
when its acceleration is
2m/sec2
, is
(a) π+√3m/sec
(b) π3+√3m/sec
(c) 2π3+√3m/sec
(d)π3+1√3m/sec
Step by step video solution for The equation of motion of a particle is s=2t^2+sin2t , where s is in metres and t is in seconds. The velocity of the particle when its acceleration is 2m/sec^2 , is (a) pi + sqrt(3)m/sec (b) pi/3+sqrt(3)m/sec (c) (2pi)/3 + sqrt(3)m/sec (d)pi/3 + 1/sqrt(3)m/sec by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
The equation of motion of particle is S=at2+bt+c.If the displcement after 1 sec is 20 m, velo0city after 2 sec is 30 m/ sec and the acceleration is 10m/se2, then
Aa+c=2bBa+c=bCa−c=bDa+c=3b - Question 2 - Select One
Position of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
A15m/sB12m/sC18m/sD6m/s - Question 3 - Select One
The acceleration of a particle, moving in a straight line, at time t is (2t+1)m/sec2 . If 4m/sec is the initial velocity of the particle then its velocity after 2 sec. is
A10cm/secB8cm/secC4cm/secDNone of these
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionThe acceleration time graph of the motion of a particle from A to B is semicircle with radius of √7 . Find the velocity of particle at t2 at it t1 velocity is 3m/sec[π=22/7] .
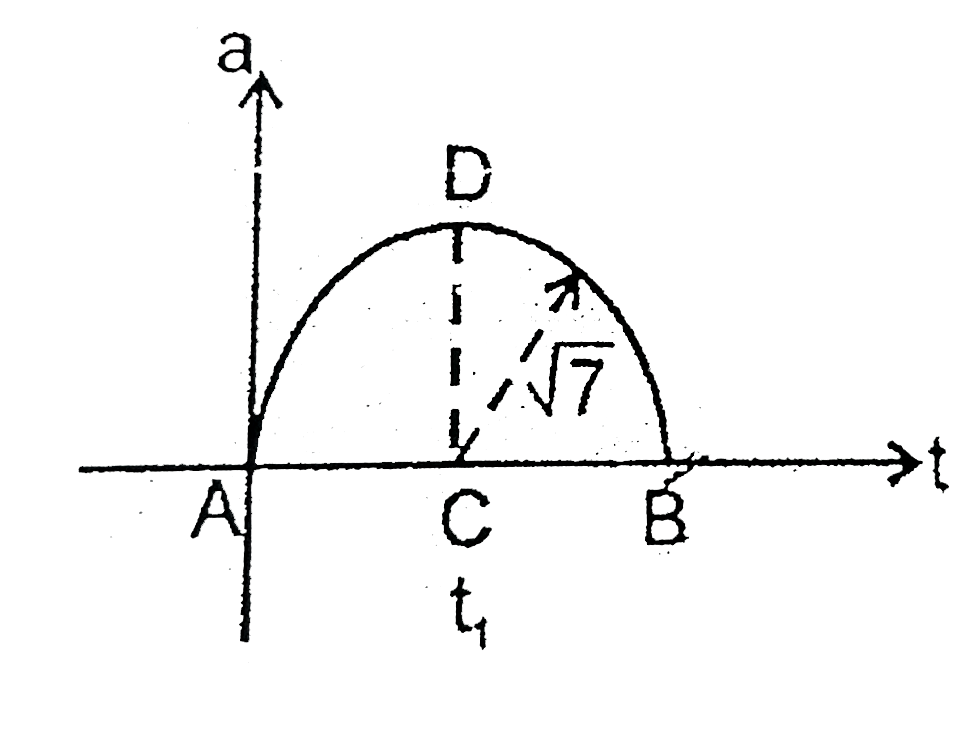 View Solution
View SolutionThe distance travelled s in metres by a particle in t second is given by s=t3+2t2+t. The speed of the particle after 1s will be
View SolutionThe initial velocity of the particle is 10m/sec and its retardation is 2m/sec2. The distance moved by the particle in 5th second of its motion is
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.View Solution
