The equations of L1andL2 are y=mxandy=nx, respectively. Suppose L1 make twice as large of an angle with the horizontal (measured counterclockwise from the positive x-axis) as does L2 and that L1 has 4 times the slope of L2. If L1 is not horizontal, then the value of the product (mn) equals:
√22
−√22
2
-2
The correct Answer is:C
Step by step video, text & image solution for The equations of L_1 and L_2 are y = mx and y = nx, respectively. Suppose L_1 make twice as large of an angle with the horizontal (measured counterclockwise from the positive x-axis) as does L_2 and that L_1 has 4 times the slope of L_2. If L_1 is not horizontal, then the value of the product (mn) equals: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - STRAIGHT LINES EXERCISE - Exercise-2 : One or More than One Answer is/are Correct
12 Videos
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - STRAIGHT LINES EXERCISE - Exercise-3 : Comprehension Type Problems
4 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
12 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
The equations of L1andL2 are y=mxandy=nx, respectively. Suppose L1 make twice as large of an angle with the horizontal (measured counterclockwise from the positive x-axis) as does L2 and that L1 has 4 times the slope of L2. If L1 is not horizontal, then the value of the product (mn) equals:
View SolutionLines L1 and L2 have slopes m and n, respectively, suppose L1 makes twice as large angle with the horizontal (mesured counter clockwise from the positive x-axis as does L2 and L1 has 4 times the slope of L2. If L1 is not horizontal, then the value of the proudct mn equals.
View Solution
Knowledge Check
The eqautions of lines L1andL2 are y=mxandy=nx, respectively. Suppose L1 makes twice as large an angle with the horizontal (measured counterclockwise from the positive x - axis) as does L2 and m = 4n, then the value of (m2+4n2)(m2−6n2) is equal to (where, n≠0)
A3B−3C2D−2The area of triangle formed by the lines l1andl2 and the x-axis is:
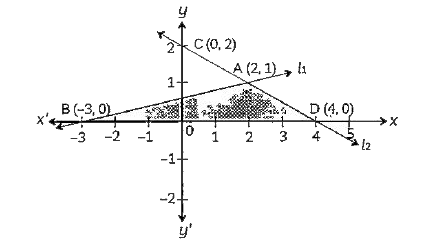 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. unitsIn Fig., there are two convex lenses L1andL2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be :
 .AF1BF2CF1+f2DF1−F2
.AF1BF2CF1+f2DF1−F2
Questions based on L1 and L2
View SolutionQuestions based on L1-L2
View SolutionIf the line of intersection of plane
P : 2x + y + z = 2 with xy plane is L1,
with zx plane is L2 and with yz plane is
L3 then the area of triangle formed by
lines L1,L2,L3 is △, then the value of △2 is equal to
View Solutionconsider three congerging lenses L1,L2andL3 having identical geometrical construction. The index of refraction of L1andL2areμ1andμ2 respectively. The upper half of the lens L3 has a refractive index μ1 and the lower half has μ2. A point object O is imaged at O1 by the lens L1andatO2 by the lens L2 placed in same position . If L2 is placed at the same place.

View SolutionThe slope of the line that bisects the angle formed by the lines l1 and l2 if l1 has a slope of 2 and l2 is a vertical line can be
View Solution
