The faces of a die bear number 0,1,2,3,4,5.
If the die is rolled twice, then find the probability that the product of the digits on the upper face is zero.
The correct Answer is:∴P(A)=n(A)n(S)=1136
Step by step video, text & image solution for The faces of a die bear number 0,1,2,3,4,5. If the die is rolled twice, then find the probability that the product of the digits on the upper face is zero. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - ASSIGNMENT - V7videos
PROBABILITY
- BOOK - UNIQUE PUBLICATIONCHAPTER - PRACTICE FOR SUBQUESTIONS EXERCISE - 2 marks Questions85videos
PRACTICE FOR SUBQUESTIONS
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS1videos
PYTHAGORS THEORM
Similar Questions
Knowledge Check
- Question 1 - Select One or More
Complete the following activity by filling the boxes:
The face of a die bear the numbers 1,3,5,7,9,11.
The die is rolled. Find the probability of getting a perfect square number on the upper face of die.AS=□B∴n(S)=□CLet A be the event of getting a perfect square number.
Then A =□ ∴n(A)=□DP(A)=n(A)n(S)=□□=□ - Question 2 - Select One
A die is rolled. What is the probability that the number appearing on the upper surface is less than 4 ?
A16B14C13D12 - Question 3 - Select One
A die is rolled. What is the probability that the number of on the upper face is less than 2?
A1B13C12D16
If one die is rolled then find the probability of each of the following events
Number on the upper face is primeView SolutionThe faces of a die bear the numbers 1,3,5,7,9,11. The die is rolled. Find the probability of getting a perfect square number on the upper face of the dice.
(i)S={1,3,5,7,9,11} (ii)∴n(S)=6
(iii) Let A be the event of getting a perfect square number. Then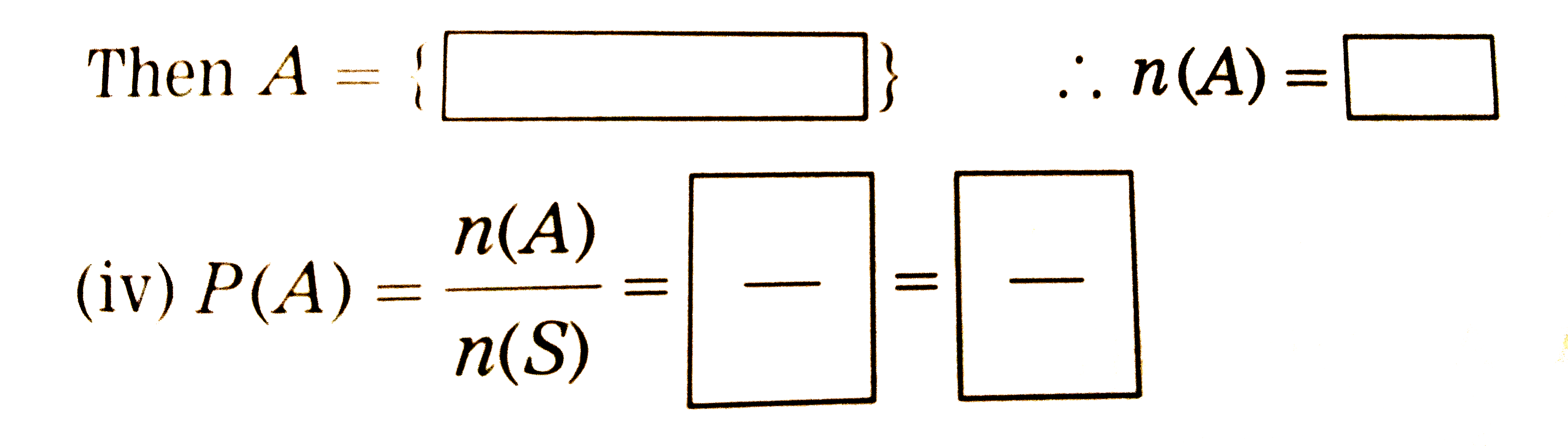
P(A)=n(A)n(S)=−=−View SolutionA die is rolled twice. Find the probability that 4 will come up exactly one time.
View SolutionIf a die is thrown, then find the probability of getting a composite number on the upper face.
View SolutionA special dice with numbers 1,-1,2,-2,0 and 3 is thrown thrice. What is the probability that the sum of the numbers occurring on the upper face is zero?
View Solution