The feasible region for a LPP is shown in Figure. Evaluate z = 4x + y at each of the corner points at this region. Find the minimum value of z, if exists.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:3
Step by step video, text & image solution for The feasible region for a LPP is shown in Figure. Evaluate z = 4x + y at each of the corner points at this region. Find the minimum value of z, if exists. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - MULTIPLE CHOICE QUESTIONS42videos
LINEAR PROGRAMMING
- BOOK - KUMAR PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - PRACTICE PAPER - 1214videos
LINEAR PROGRAMMING
- BOOK - KUMAR PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK11videos
LINEAR PROGRAMMING
- BOOK - KUMAR PRAKASHANCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE PAPER - 2 (SECTION - D)2videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - KUMAR PRAKASHANCHAPTER - MATRICES EXERCISE - Practice Paper - 3 (Section - D)1videos
MATRICES
Similar Questions
Solution set of the inequality 2x+y>5 is ………
03:16View SolutionThe correct points of the feasible region determined by the following system of linear inequalities, 2x+y≤10,x+3y≤15,x,y≥0, are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p,q>0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is ..........
02:11View SolutionSolve the following linear programming problem graphically :
Maximise Z = 4x + y …(1)
subject to the constraints :
x+y≤50 …(2)
3x+y≤90…(3)"
x≥0,y≥0 ...(4)03:53View SolutionProve that :
cot−1(√1+sinx+√1−sinx√1+sinx−√1−sinx)=x2,x∈(0,π4)02:45View SolutionFor matrix A=⎡⎢⎣11112−32−13⎤⎥⎦ . Prove that , A3−6A2+5A+11I=0. Hence find A−1 using it .
02:17View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists
 05:41View Solution
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
03:28View SolutionFind the area of the shaded region, given that the radius of each circle is equal to 5 cm.
02:31View SolutionMatch the following Column A to Column B
 02:21View Solution
02:21View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionFind the area of figure given below.
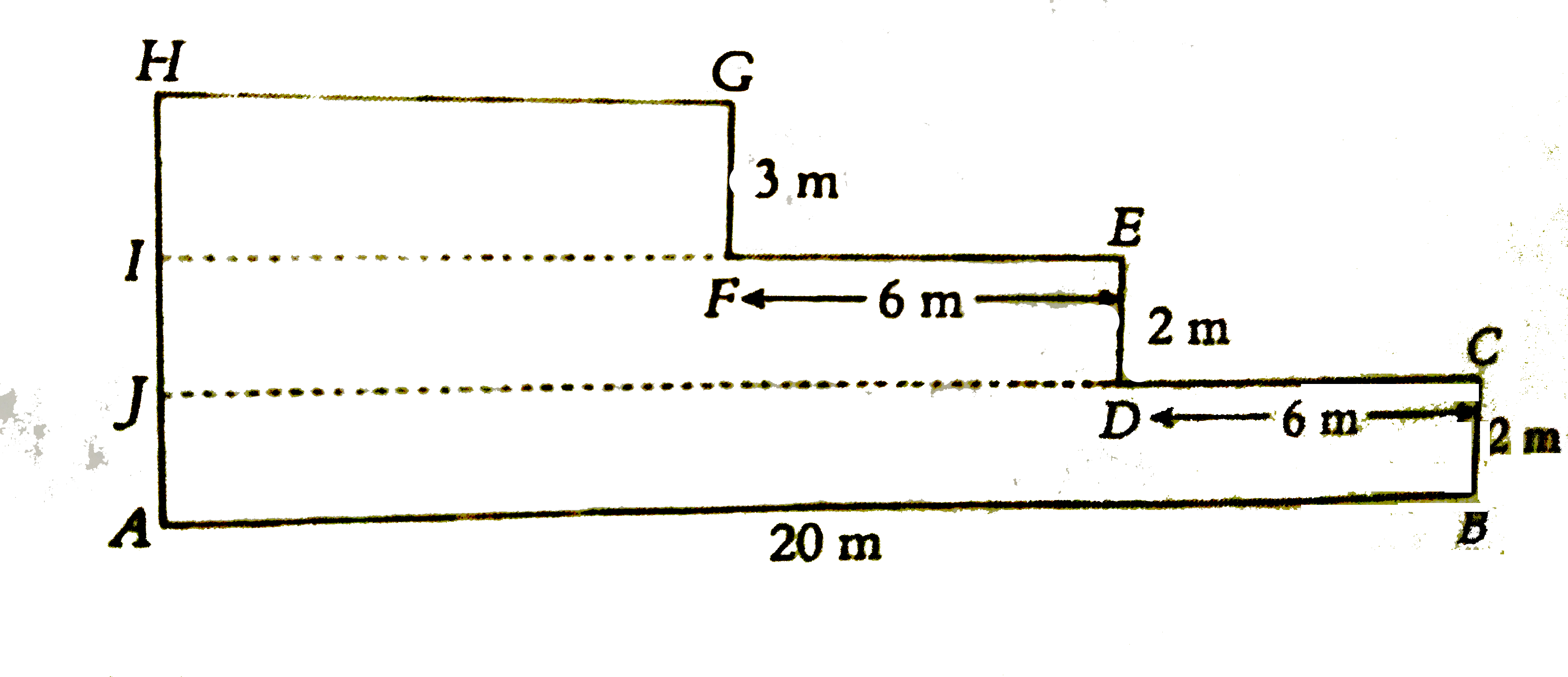 02:10View Solution
02:10View SolutionFind the perimeter of the figure given below.
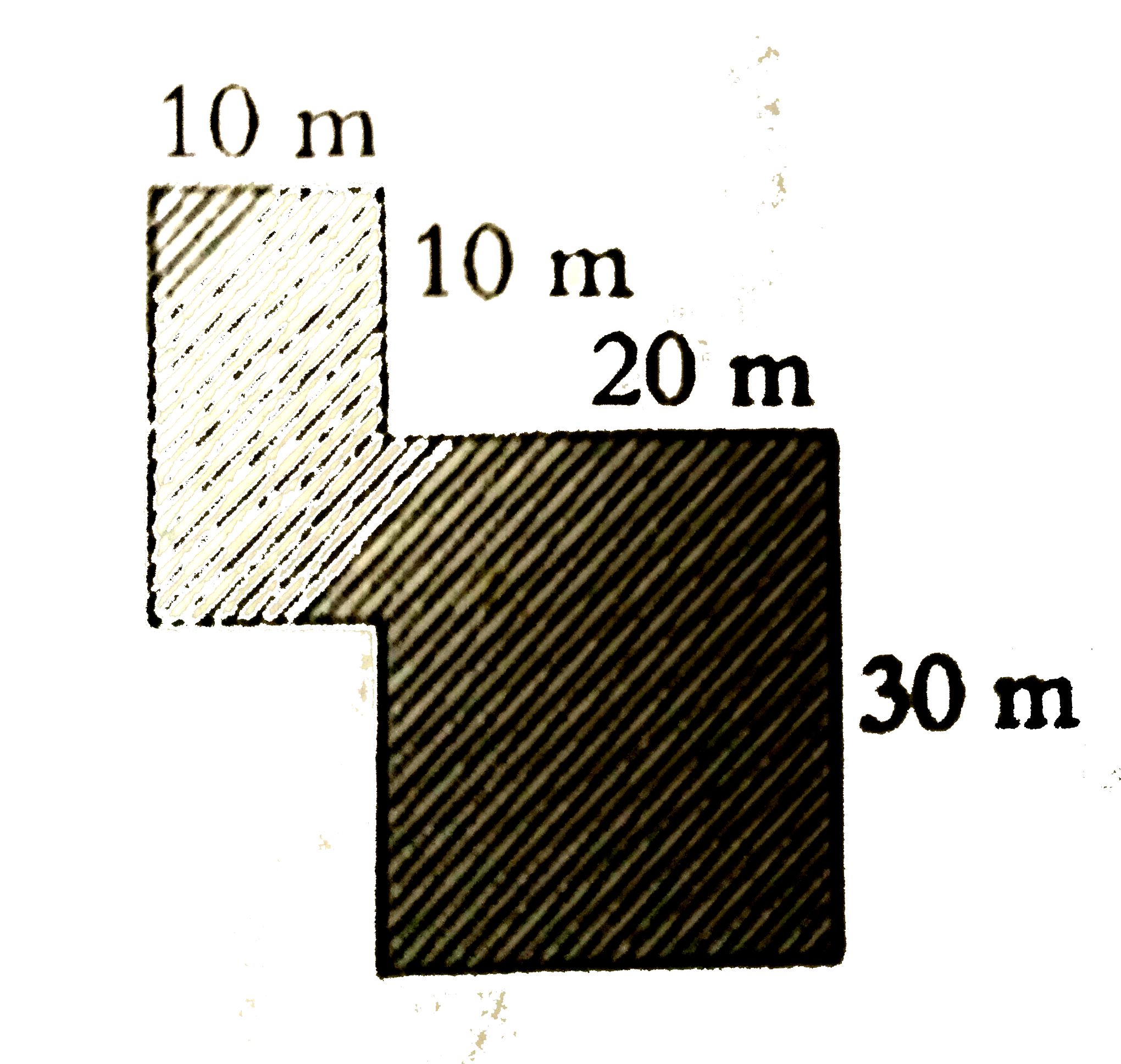 04:23View Solution
04:23View SolutionFind the area of the figure given below.
 01:13View Solution
01:13View SolutionThe inequation represented by the graph given below is :
01:32View SolutionThe inequation that best describes the graph given below is _________
04:05View Solution

