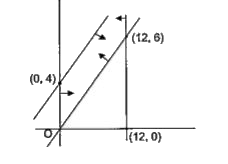
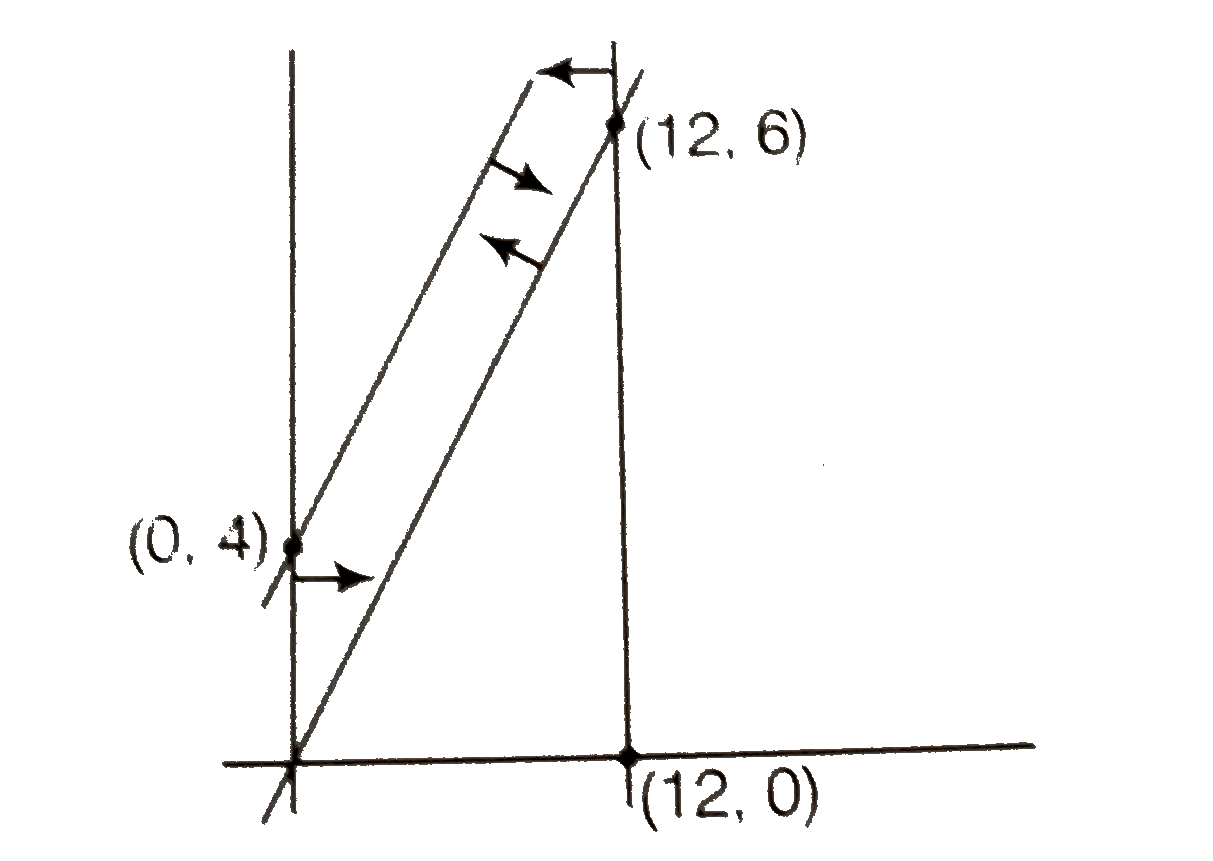
The feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
The correct Answer is:B
Step by step video & image solution for The feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
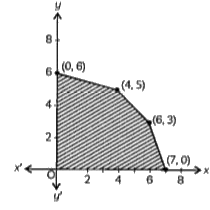
The feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
 A0B8C12D−18
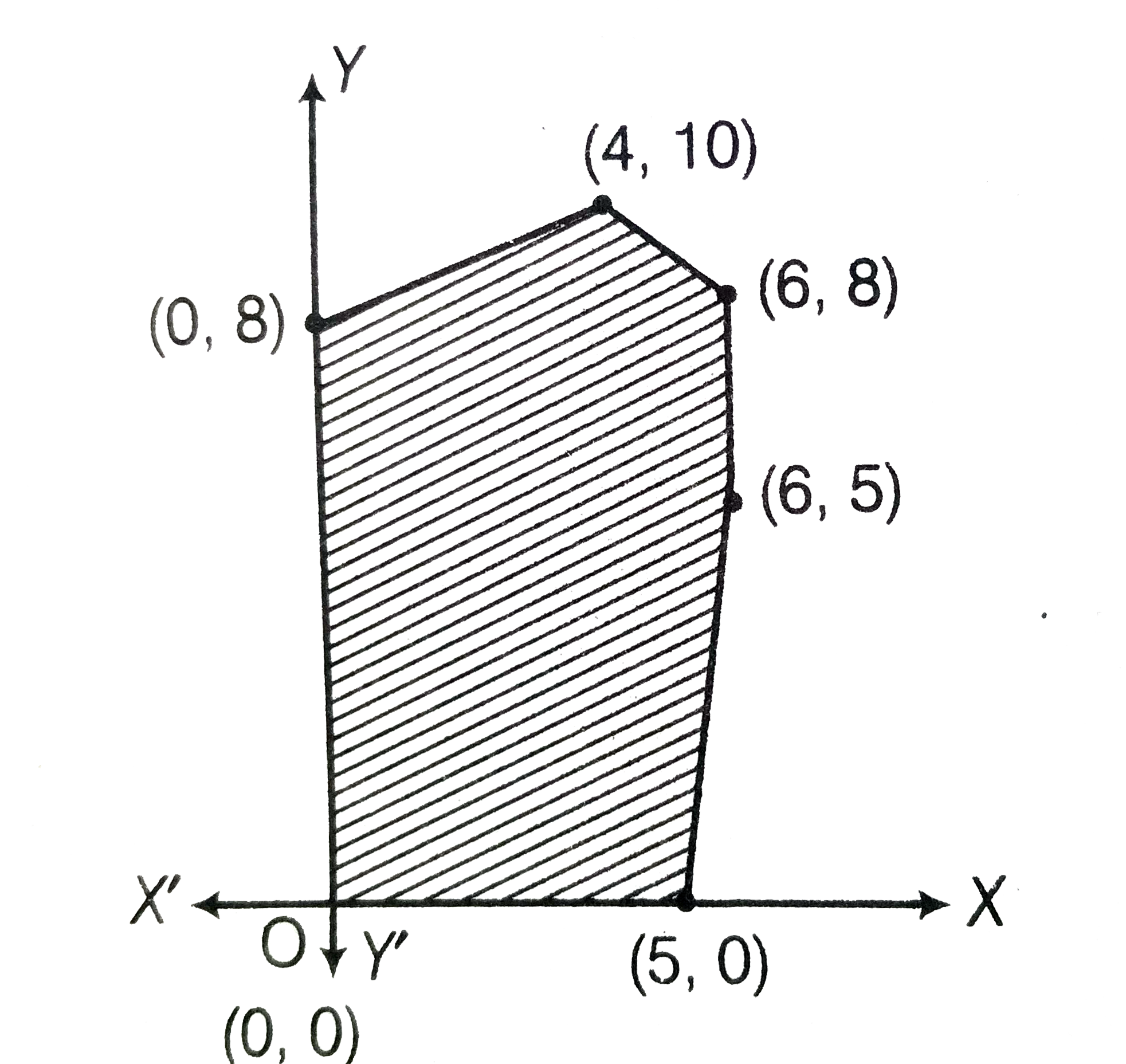
A0B8C12D−18The feasible solution for a LPP is shown in following figure. Let Z=3x−4y be the objective function, Minimum of Z occurs at
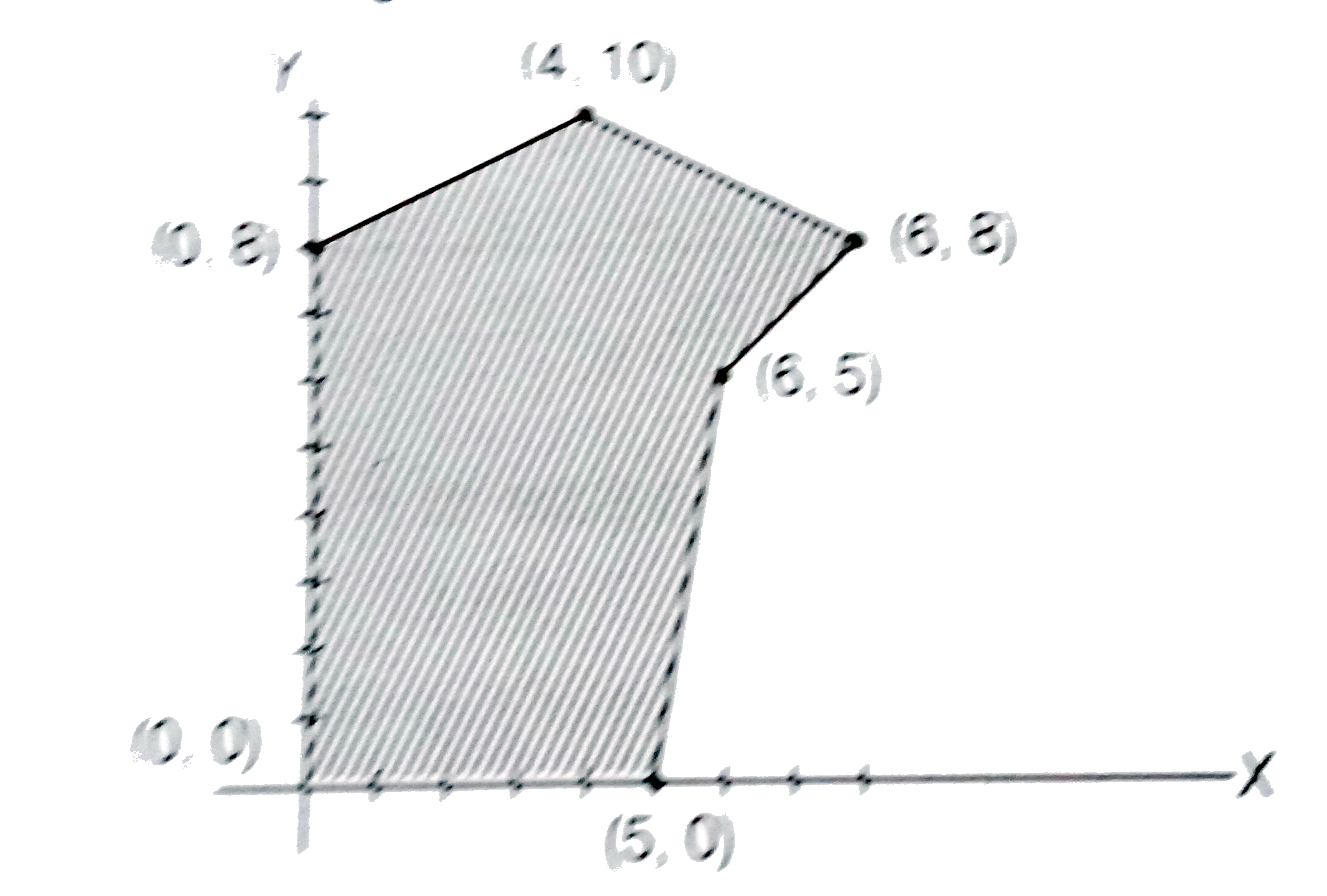 A(0,0)B(0,8)C(5,0)D(4,10)
A(0,0)B(0,8)C(5,0)D(4,10)Corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F=4x+6y be the objective function. Determine the minimum value of F occurs at
Aonly (0,2)Bonly (3,0)Cthe mid point of the line segment joining the points (0,2) and (3,0)Dany point of the line segment joining the points (0,2) and (3,0)
The feasible solution for a LPP is hown as below,
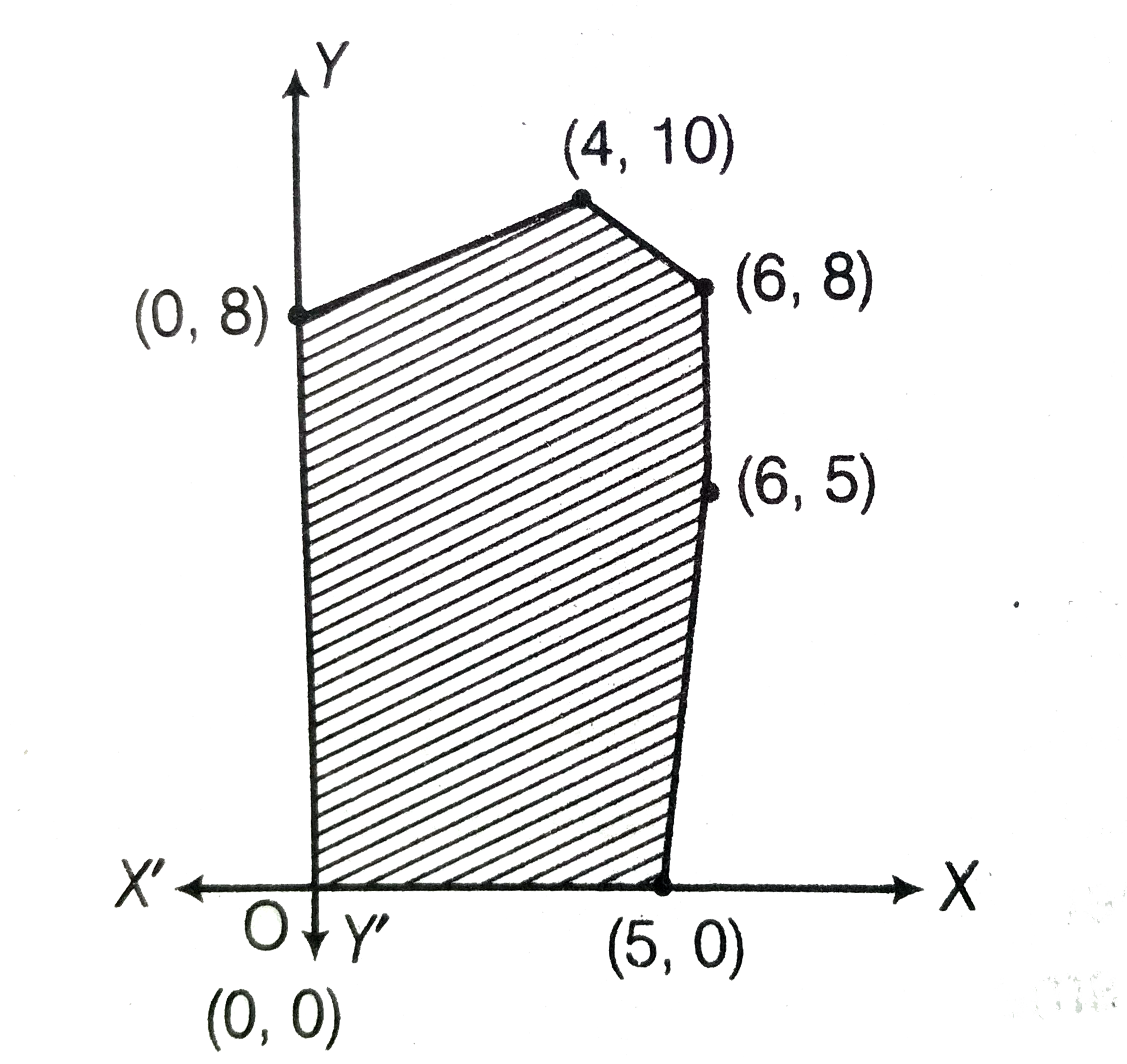
Let Z =3x -4y be the objective function . Then, Minimum of Z occurs at
View SolutionThe feasible region of an LPP is shown in the figure. If z=3x+9y ,then the minimum value of z occurs at
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists
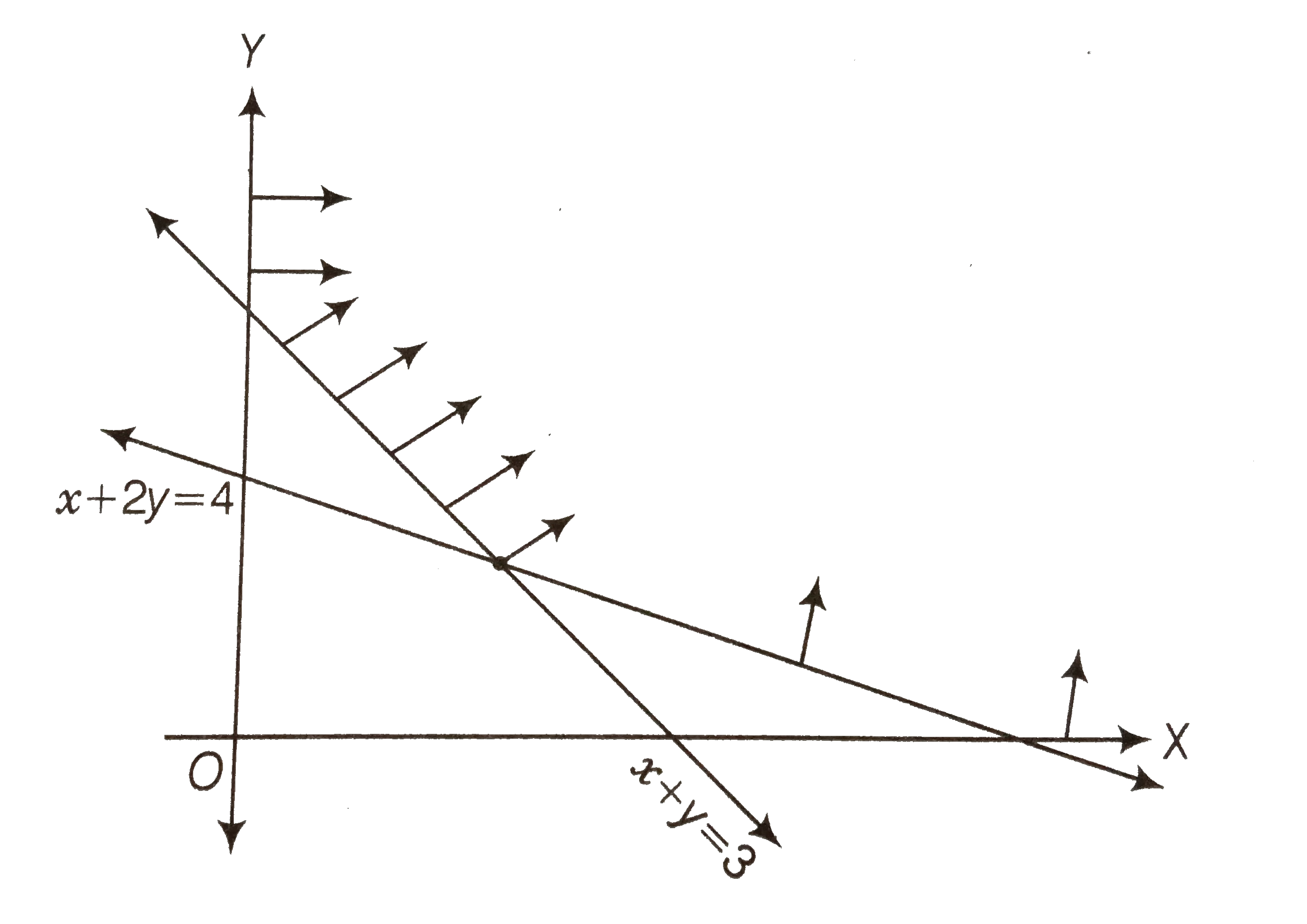
View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View Solution