Doubtnut Promotions Sticky

In the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:N/a

If the feasible region for a LPP is unbouded, then the optimal value of the objective fucnction Z=ax+by may or may not exist.

|
Updated on:21/07/2023
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

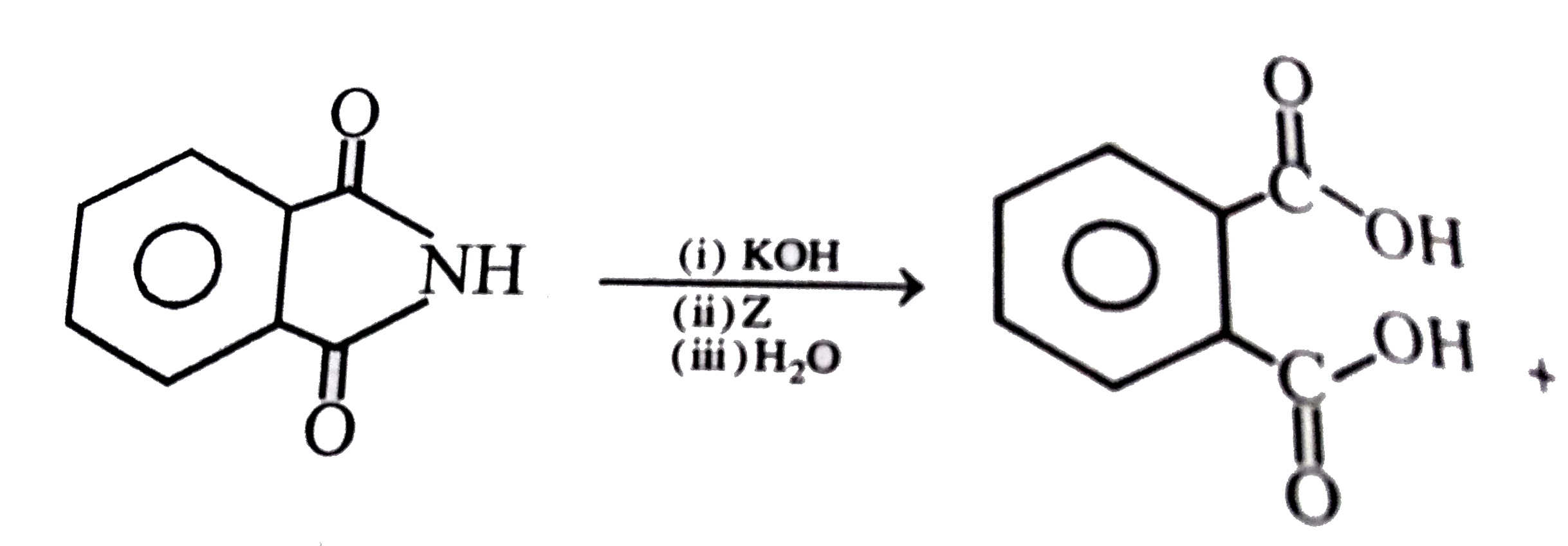
    ocr_image
    Z may not be:

    ACH3−Cl
    BCH3H∣C∣CH3−Cl
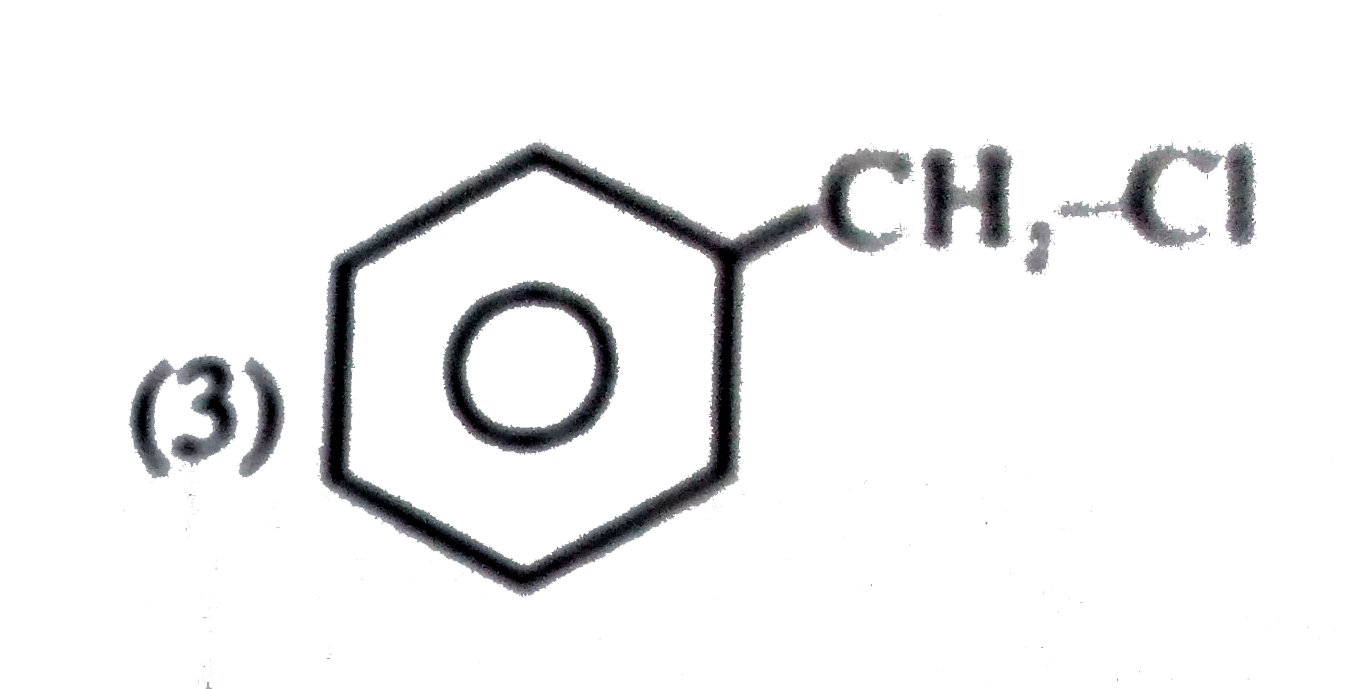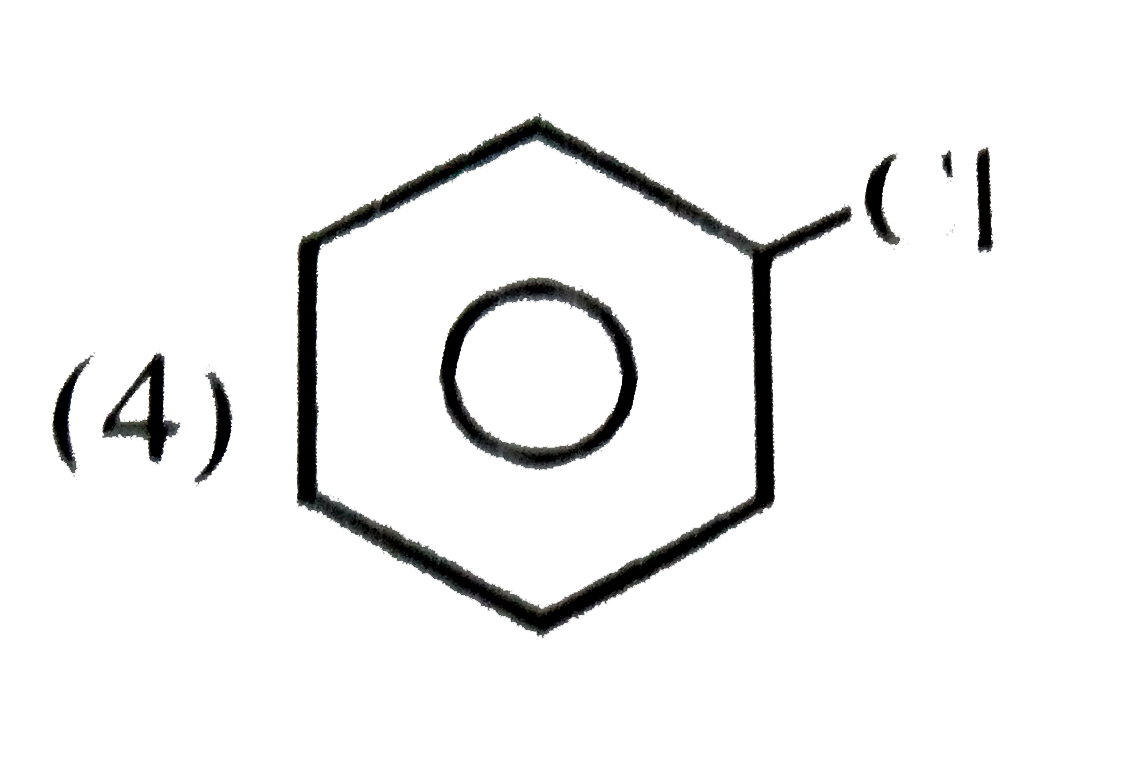
    Cocr_image
    Docr_image
  • Question 2 - Select One

    Consider the following statements
    I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
    II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
    Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
    IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
    Which of the following statements are true?

    AI and IV
    BII and III
    CI and III
    DII and IV
  • Question 3 - Select One

    The optimal value of the objective function is attained at the points

    Agiven by intersectionn of inequations with axis only
    Bgiven by intersection of inequations with X-axis only
    Cgiven by corner points of the feasible region
    Dnone of the above