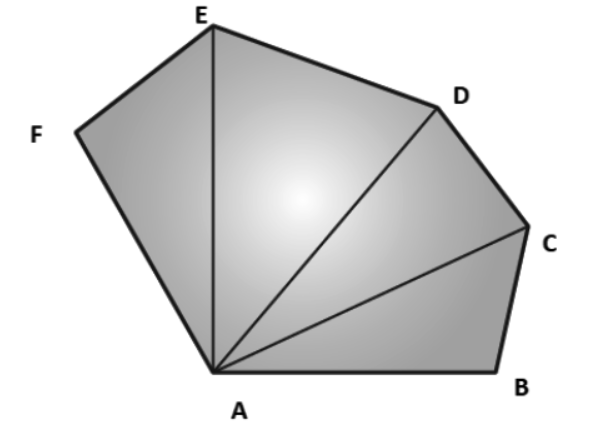
The fig.16 has been obtained by using two triangles. Find ∠A+∠B+∠C+∠D+∠E+∠F.
To solve the problem of finding the sum of the angles ∠A+∠B+∠C+∠D+∠E+∠F from the given figure, we can follow these steps:
1. Identify the Triangles:
- From the figure, we can see that there are two triangles involved: Triangle ACE and Triangle BDF.
2. Apply the Angle Sum Property:
- We know that the sum of the angles in any triangle is always 180∘.
- For Triangle ACE, we can write:
∠A+∠C+∠E=180∘(Equation 1)
3. Apply the Angle Sum Property to the Second Triangle:
- For Triangle BDF, we can similarly write:
∠B+∠D+∠F=180∘(Equation 2)
4. Add the Two Equations:
- Now, we will add Equation 1 and Equation 2:
(∠A+∠C+∠E)+(∠B+∠D+∠F)=180∘+180∘
- This simplifies to:
∠A+∠B+∠C+∠D+∠E+∠F=360∘
5. Conclusion:
- Therefore, the sum of the angles ∠A+∠B+∠C+∠D+∠E+∠F is 360∘.
Final Answer:
∠A+∠B+∠C+∠D+∠E+∠F=360∘
- From the figure, we can see that there are two triangles involved: Triangle ACE and Triangle BDF.
- We know that the sum of the angles in any triangle is always 180∘.
- For Triangle ACE, we can write:
∠A+∠C+∠E=180∘(Equation 1)
- For Triangle BDF, we can similarly write:
∠B+∠D+∠F=180∘(Equation 2)
- Now, we will add Equation 1 and Equation 2:
(∠A+∠C+∠E)+(∠B+∠D+∠F)=180∘+180∘
- This simplifies to:
∠A+∠B+∠C+∠D+∠E+∠F=360∘
- Therefore, the sum of the angles ∠A+∠B+∠C+∠D+∠E+∠F is 360∘.
∠A+∠B+∠C+∠D+∠E+∠F=360∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
∠A,∠B,∠Care three angles of a triangle. If ∠A−∠B=15∘,∠B−∠C=30∘, then ∠A,∠Band∠C are
A80∘,60∘,40∘B70∘,50∘,60∘C80∘,65∘,35∘D80∘,55∘,45∘
Fill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……View SolutionIn Fig.87, the corresponding arms of ∠ABC and ∠DEF are parallel. If ∠ABC=750, find the ∠DEF.
View SolutionTwo triangles ABC and DEF such that ∠A=∠D,∠B=∠Eand∠C=∠F. Then
View SolutionIf any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent. GIVEN : Two sABC and DEF such that ∠A=∠D,∠B=∠E,BC=EF TO TROVE : ABC≅DEF
 View Solution
View SolutionTwo triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. GIVE : Two sABC and DEF such that ∠B=∠E,∠C=∠F and BC=EF TO PROVE : ABC≅DEF
View SolutionIn a ΔABC; if 2∠A=3∠B=6∠C; Determine ∠A;∠Band∠C
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
 View Solution
View Solution