The figure shows a portion of the graph y=2x−4x3. The line y=c is such that the areas of the regions marked I and II are equal. If a, b are the x-coordinates of A,B respectively, then a+b equals-

A
2√7
B
3√7
C
4√7
D
5√7
Video Solution
Text Solution
The correct Answer is:A
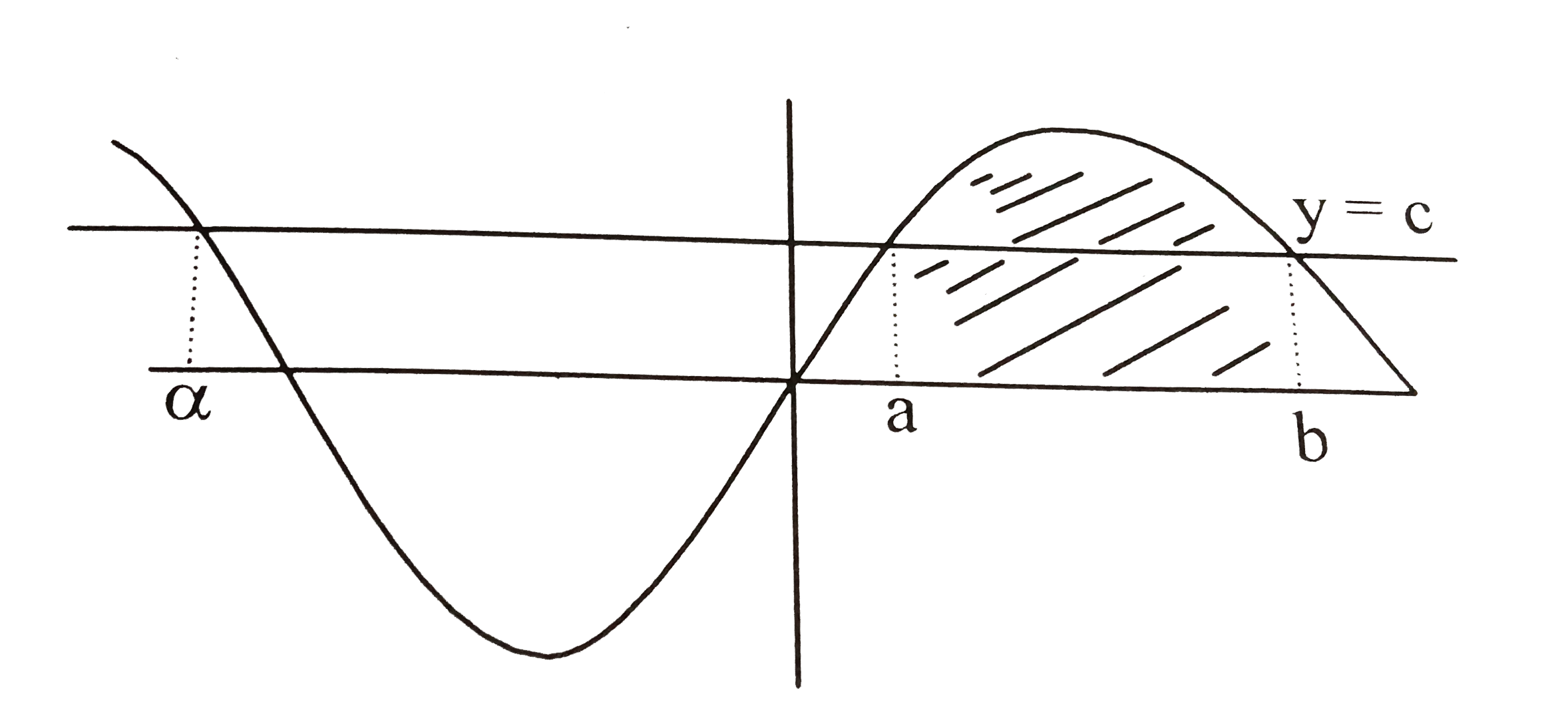
fba(2x−4x3)dx=2(b−a)c
(x2−x4)ba=2(b−a)c
(a+b)(1−(a2+b2))=2c
(a+b)(1−(a+b)2+2ab)=ac . . .(1)
again 2x−4x3=c
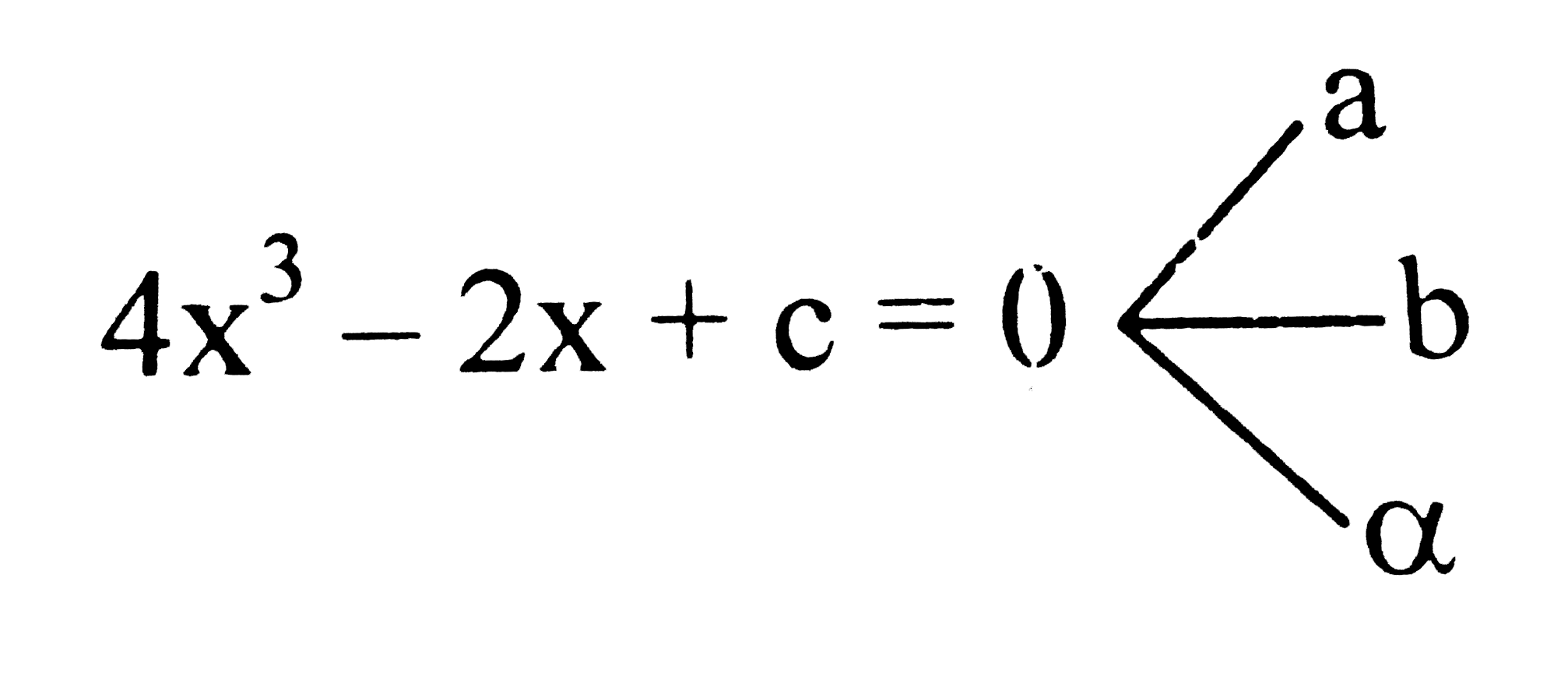
a+b+α=0 clearlya+b=−a . . .(2)
ab+(a+b)α=−12 ab=α2−12 . . .(3)
abα=−c4 c=−4α(a2−12) . . .(4)
put value of (a+b), ab, c from eq. (2), (3), (4) in equation (1) and solve it
{1−α2+2(α2−12)}=−8α(α2−12)
1−α2+2α2−1=8α2−4
α2=8α2−4
7α2=4
α=2√7
|
Similar Questions
Knowledge Check
The area of the region bounded by y – x = 2 and x2=y is equal to
A163B23C92D43The area of the region bounded by the curve y=x2 and y =|x| is equal to
A53 sq. unitsB13 sq. unitsC53 sq. unitsD16 sq. unitThe area of the region bounded by the curve y=x2 and y = x is equal to
A92 sq. unitsB72 sq. unitsC(e−1e)2 sq. unitsD16 sq. units
The area of the triangle formed by the line xa+yb=1 with the coordinate axes is
View SolutionWrite the area of the figure formed by the lines a|x|+b|y|+c=0.
View SolutionThe area of the region bounded by the curves y=xex,y=ex and the lines x=±1, is equal to
View SolutionThe area of the region bounded by y=x2 and y = 4x , for x between 0 and 1 is equal to
View SolutionIf the line, y=mx bisects the area of the region {(x,y):0≤x≤32,0≤y≤1+4x−x2}, then m equals:
View Solution