The figure shows a and the parabola . The ratio of the area of the to the area of the region AOB of the parabola is equal to
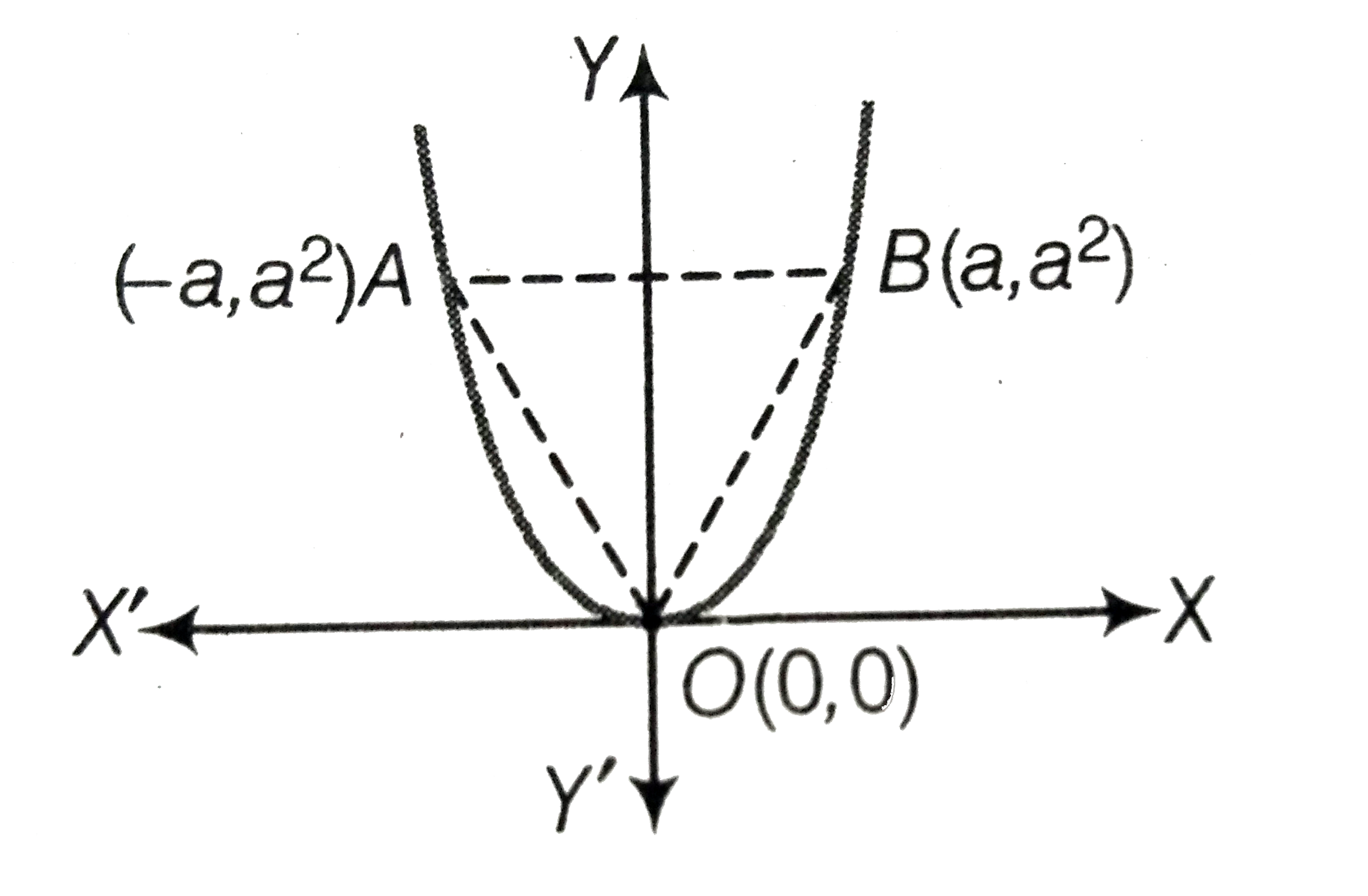
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
Area of curve
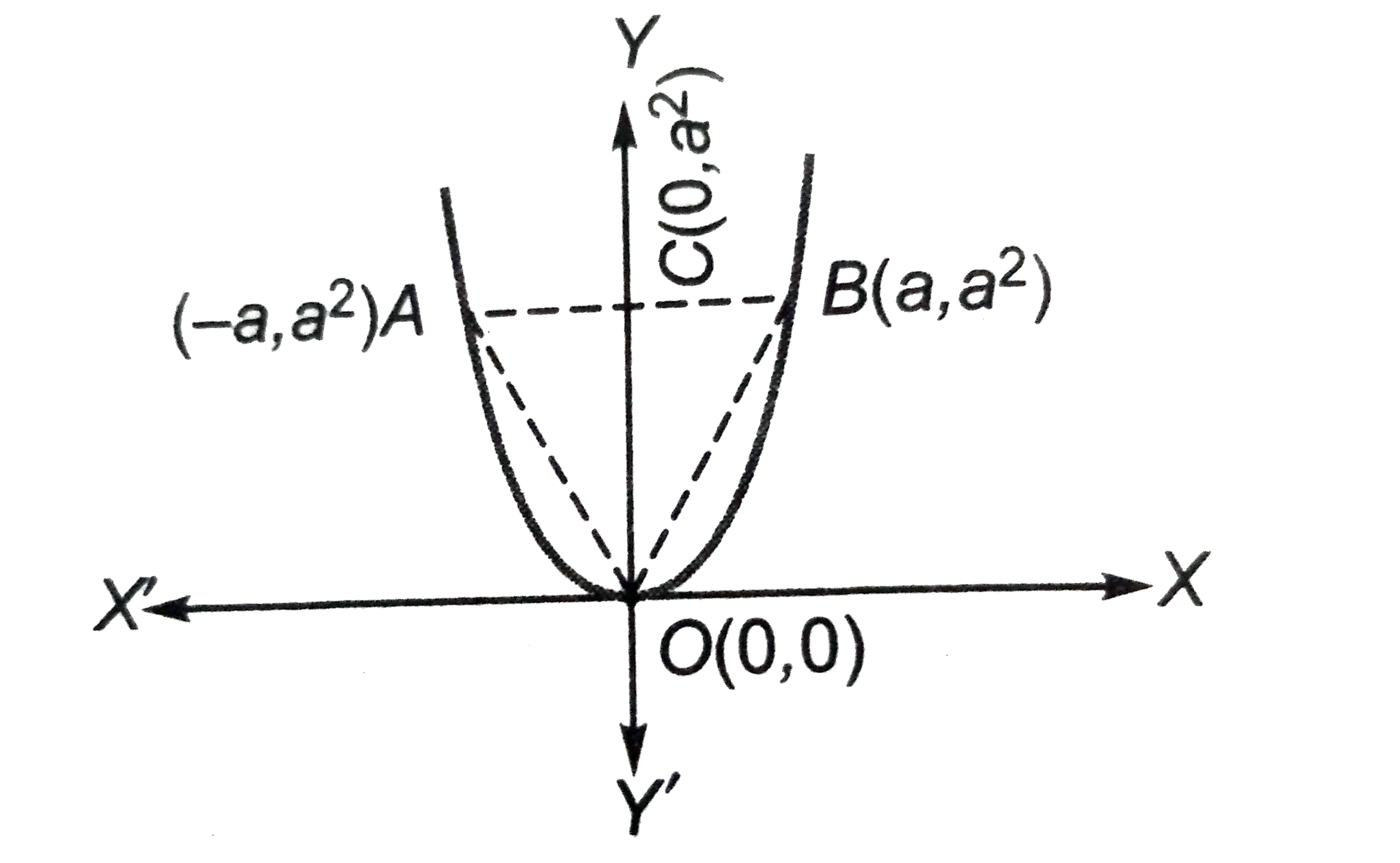
Now, area of
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:MHT CET Corner
Explore 6 Videos
- APPLICATIONS OF DEFINITE INTEGRALS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DEFINITE INTEGRALS Exercise:MHT CET Corner
Explore 6 Videos
- APPLICATIONS OF DERIVATIVESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:APPLICATIONS OF DERIVATIVESExercise:MHT CET CORNER
Explore 21 Videos
Similar Questions
Knowledge Check
The area of the region bounded by y – x = 2 and x2=y is equal to
A163B23C92D43The area of the region bounded by the parabola y=x2 and the line y = 4x is
A323sq.unitsB163sq.unitsC83sq.unitsD43sq.units
Find the area of the region bounded by: the parabola y=x2 and the line y=x
View SolutionFind the area of the region between the parabola x=y2−6y and the line x=−y
View SolutionFind the area of the region bounded by the parabola y2=8x and the line x=2
View SolutionFind the area of the region between the parabola x=4y−y2 and the line x=2y−3.
View SolutionFind the area of the region bounded by the two parabolas y=x2and y2=x.
View SolutionFind the area of the region bounded by the parabola y2=2x and the line x−y=4
View Solution
