The focus of a parabolic mirror as shown in figure is at a distance of 5 cm from its vertex. If the mirror is 45 cm deep, find the distance AB
To solve the problem, we need to find the distance AB for a parabolic mirror where the focus is at a distance of 5 cm from its vertex and the mirror is 45 cm deep.
1. Understand the Geometry of the Parabola:
The parabola opens to the right, and its vertex is at the origin (0, 0). The focus of the parabola is located at (a, 0), where 'a' is the distance from the vertex to the focus. Here, a = 5 cm.
2. Write the Equation of the Parabola:
The standard equation of a parabola that opens to the right is given by:
y2=4ax
Substituting the value of 'a':
y2=4⋅5⋅x
Simplifying this, we get:
y2=20x
3. Determine the Depth of the Mirror:
The depth of the mirror is given as 45 cm. This depth corresponds to the x-coordinate of the point where the mirror ends, which is at x = 45 cm.
4. Find the y-coordinate at x = 45 cm:
Substitute x = 45 into the equation of the parabola:
y2=20⋅45
Calculating this gives:
y2=900
Taking the square root of both sides:
y=√900=30 cm
5. Calculate the Distance AB:
The distance AB is twice the y-coordinate since the parabola is symmetric about the x-axis:
AB=2y=2⋅30=60 cm
Final Answer:
The distance AB is 60 cm.
The parabola opens to the right, and its vertex is at the origin (0, 0). The focus of the parabola is located at (a, 0), where 'a' is the distance from the vertex to the focus. Here, a = 5 cm.
The standard equation of a parabola that opens to the right is given by:
y2=4ax
Substituting the value of 'a':
y2=4⋅5⋅x
Simplifying this, we get:
y2=20x
The depth of the mirror is given as 45 cm. This depth corresponds to the x-coordinate of the point where the mirror ends, which is at x = 45 cm.
Substitute x = 45 into the equation of the parabola:
y2=20⋅45
Calculating this gives:
y2=900
Taking the square root of both sides:
y=√900=30 cm
The distance AB is twice the y-coordinate since the parabola is symmetric about the x-axis:
AB=2y=2⋅30=60 cm
The distance AB is 60 cm.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - MISCELLANEOUS EXERCISE9videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.115videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.320videos
CONIC SECTIONS
- BOOK - NCERT ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions75videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.14videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
Similar Questions
The focus of a parabolic mirror as shown in the figure alongside is at a distance of 6cm from its vertex. If the mirror is 20cm deep, find the distance BC.
View SolutionThe focus of a parabolic mirror is at a distance of 6 cm from its vertex. If the mirror is 20 cm deep, find the distance LM.
View SolutionA concave mirror forms an image of the sun at a distance of 12 cm from it.
View SolutionA parabola reflector is 15 cm deep and its focus is at a distance of 5 cm from its vertex. Find the diameter of the reflector.
View SolutionA slab of glass, of thickness 6 cm and refractive index μ=1.5 is placed in front of a concave mirror as shown in the figure. If the radius of curvature of the mirror is 40 cm and the reflected image coincides with the object, then the distance of the object from the mirror is
 View Solution
View SolutionA square mnqp is kept between F and C on the principal axis of a concave mirror as shown in figure . Find a rough image of this object.The focal length of mirror is 30cm & distance of object is 40cm.
 View Solution
View SolutionInterference effects are produced at point P on a screen as a result of direct rays from a 500 nm source and reflected rays from a mirror, as shown in figure. If the sources is 100m to the left of the screen and 1.00 cm above the mirror, find the distance y (in milimeters) to the first dark band above the mirror.
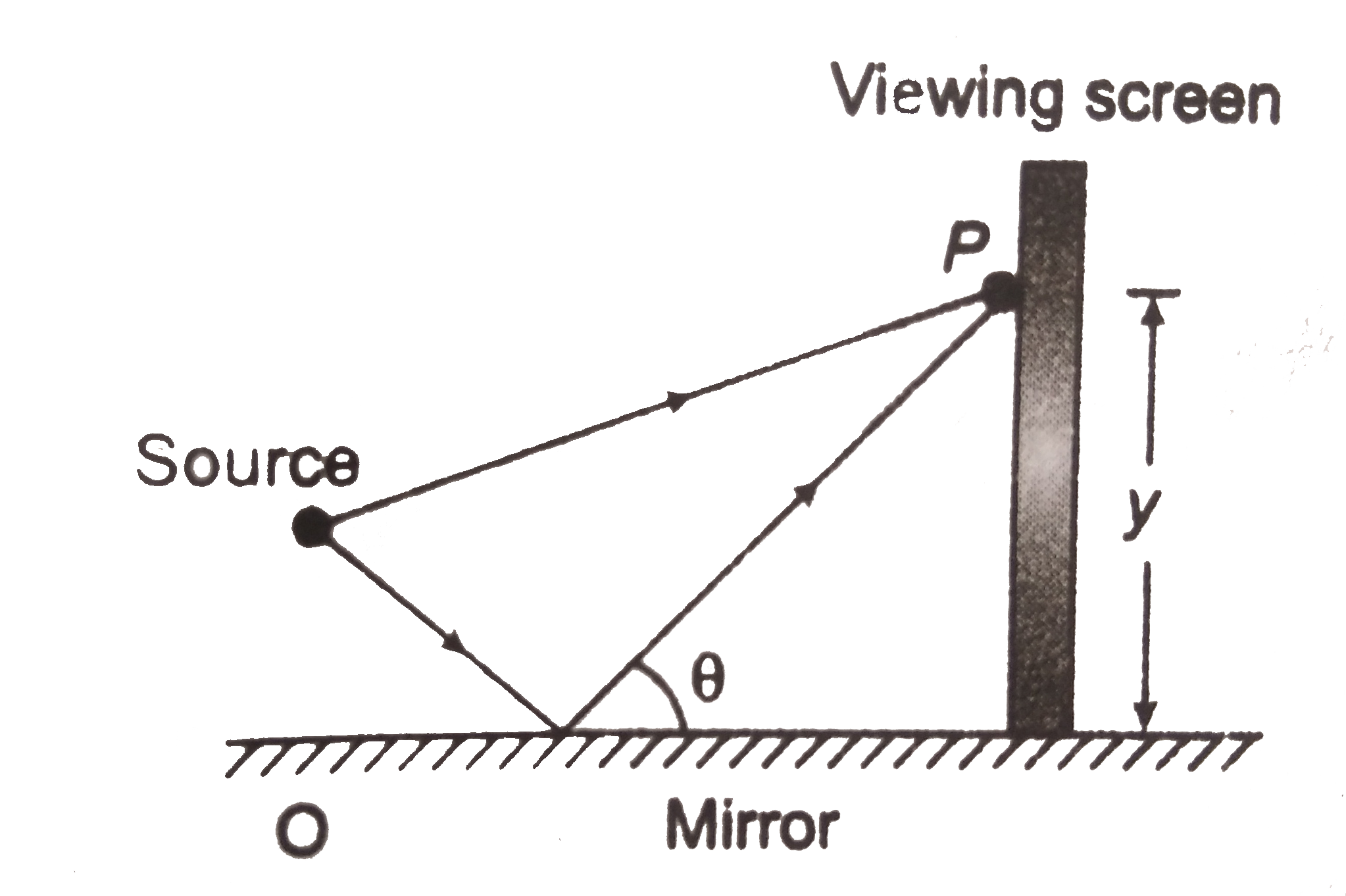 View Solution
View SolutionThe focal length of a convex mirror is 40 cm. A point source of light is kept at distance 40 cm from the mirror. Find the distance of image from the mirror.
View SolutionConcave mirror forms the real image of a point source lying on the optical axis at a distance of 50 cm from the mirror. The focal length of the mirror is 25 cm. The mirror is cut into and its halves are drawn a distance of 1 cm apart in a direction perpendicular to the optical axis. How will the image formed by the halves of the mirror be arranged?
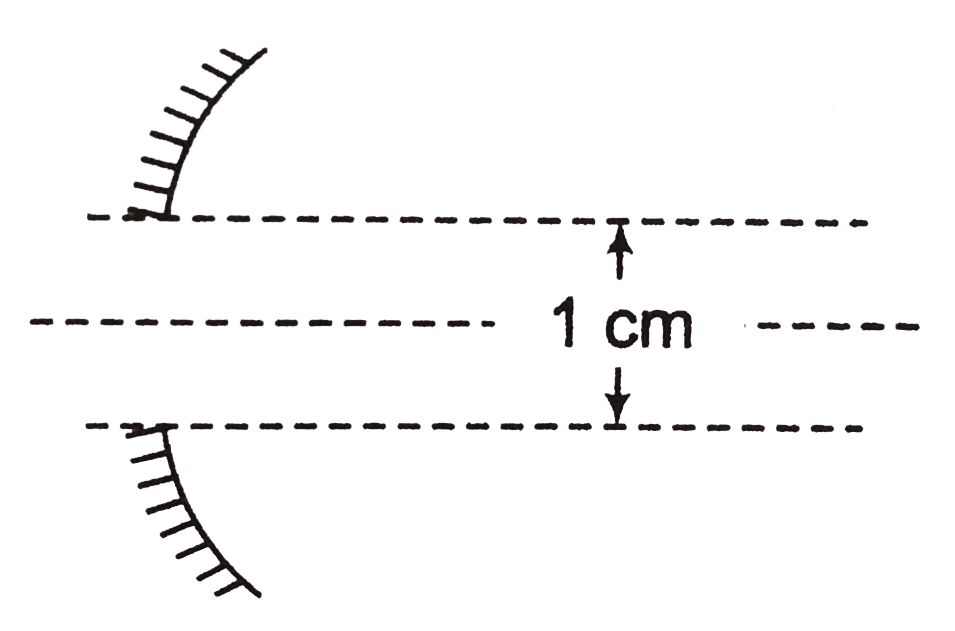 View Solution
View SolutionAn object of height 1cm is kept perpendicular to the principle axis of a convex mirror of radius of curvature 20cm. IF the distance of the object form the mirror is 20cm then the distance (in cm) between heads of the image and the object will be:
View Solution

