The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

We know that the Mean, (x) = a + (Σfᵢuᵢ/Σfᵢ) × h
Mode = l + [(f₁ - f₀) / (2f₁ - f₀ - f₂)] × h
and Median = l + [(n/2 - cf)/f] × h
So,let h=20 and a=135
From the table, Σfᵢ =68 and Σfᵢuᵢ = 7
Mean (x) = a + (Σfᵢuᵢ/Σfᵢ) × h
= 135+(768)×20
= 135+14068
= 135+2.05
= 137.05
Now,
From the table, it can be seen that the maximum class frequency is 20 which belongs to class interval 125−145.
Modal class = 125−145
The Lower limit of the modal class, l = 125
The frequency of modal class, f₁ = 20
The frequency of class preceding modal class, f₀ = 13
The frequency of the class succeeding the modal class, f₂ = 14
so,
Mode = l + [(f₁ - f₀)/(2f₁ - f₀ - f₂)] × h
= 125+[20−132×20−13−14]×20
= 125+[740−27]×20
= 125+(713)×20
= 125+14013
= 125+10.76
= 135.76
From the table, we get
n = 68⇒ n/2 = 34
So,
Cumulative frequency(cf) just greater than 34 is 42, which belongs to class-interval 125−145.
So, median class = 125−145
The Lower limit of median class, l = 125
The frequency of median class, f = 20
The Cumulative frequency of class preceding median class, cf = 22
Median = l + [(n/2 - cf)/f] × h
= 125+[34−2220]×20
=125+12
= 137
So,mean=137.05 mode=135.76 and median=137.
So, mean > median > mode
Similar Questions
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.
 View Solution
View SolutionFind the mean, median and mode of the following data
 View Solution
View SolutionThe following distribution gives the monthly consumption of consumers of a locality. Find the median of the distribution
 View Solution
View SolutionFind the mean, median and mode of the following data :
View SolutionFind the mean, median and mode of the following data :
 View Solution
View SolutionElectricity Consumption problem

The following frequency distribution gives the monthly consumption of consumers of a locality.
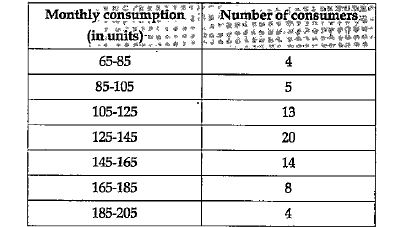
What is the mean of upper limits of median and modal class?View SolutionFind the mean, median and mode of the following data:
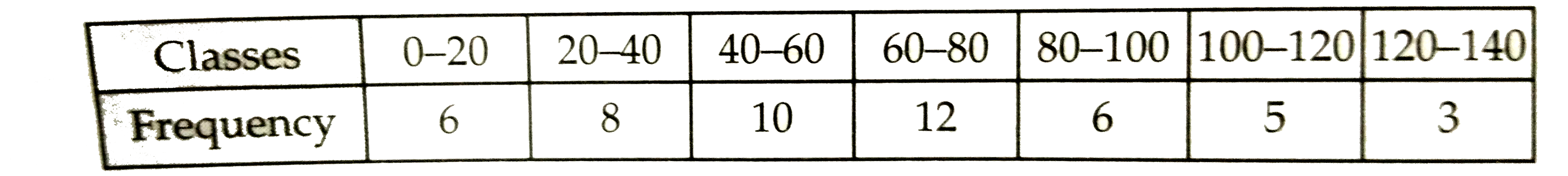 View Solution
View SolutionFind the mean, median and mode of the following data.
 View Solution
View SolutionElectricity Consumption problem
The following frequency distribution gives the monthly consumption of consumers of a locality.
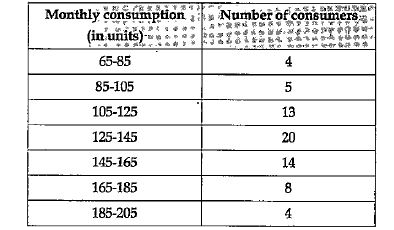
What is the width of the class?View SolutionFind the mean, median, and mode for the follow ing data.
 View Solution
View Solution

