The following table gives the distribution of the life time of 400 neon lamps: Lite time: (in hours) Number of lamps 1500-2000 14 2000-2500 56 2500-3000 60 3000-3500 86 3500-4000 74 4000-4500 62 4500-5000 48 Find the median life.
To find the median life of the neon lamps from the given distribution, we will follow these steps:
Step 1: Create a cumulative frequency table
We need to calculate the cumulative frequency for the given data.
| Lifetime (in hours) | Number of lamps (Frequency) | Cumulative Frequency |
|----------------------|----------------------------|----------------------|
| 1500 - 2000 | 14 | 14 |
| 2000 - 2500 | 56 | 14 + 56 = 70 |
| 2500 - 3000 | 60 | 70 + 60 = 130 |
| 3000 - 3500 | 86 | 130 + 86 = 216 |
| 3500 - 4000 | 74 | 216 + 74 = 290 |
| 4000 - 4500 | 62 | 290 + 62 = 352 |
| 4500 - 5000 | 48 | 352 + 48 = 400 |
Step 2: Find N and N/2
The total number of lamps (N) is 400. To find N/2:
N/2=400/2=200
Step 3: Locate the median class
We need to find the class interval where the cumulative frequency is greater than or equal to 200. From the cumulative frequency table, we see:
- The cumulative frequency just before 200 is 130 (for the class 2500 - 3000).
- The cumulative frequency that exceeds 200 is 216 (for the class 3000 - 3500).
Thus, the median class is 3000 - 3500.
Step 4: Identify the values needed for the median formula
For the median class (3000 - 3500):
- L (lower boundary of median class) = 3000
- F (frequency of median class) = 86
- CF (cumulative frequency of the class preceding the median class) = 130
- H (width of the median class) = 3500 - 3000 = 500
Step 5: Apply the median formula
The formula for the median in a grouped frequency distribution is:
Median=L+(N/2−CFF)×H
Substituting the values:
Median=3000+(200−13086)×500
Step 6: Calculate the median
First, calculate N/2−CF:
N/2−CF=200−130=70
Now substitute into the formula:
Median=3000+(7086)×500
Calculating 7086:
7086≈0.813
Now calculate:
0.813×500≈406.5
Finally, add this to 3000:
Median≈3000+406.5=3406.5
Final Answer
The median life of the neon lamps is approximately 3406.5 hours.
We need to calculate the cumulative frequency for the given data.
|----------------------|----------------------------|----------------------|
| 1500 - 2000 | 14 | 14 |
| 2000 - 2500 | 56 | 14 + 56 = 70 |
| 2500 - 3000 | 60 | 70 + 60 = 130 |
| 3000 - 3500 | 86 | 130 + 86 = 216 |
| 3500 - 4000 | 74 | 216 + 74 = 290 |
| 4000 - 4500 | 62 | 290 + 62 = 352 |
| 4500 - 5000 | 48 | 352 + 48 = 400 |
The total number of lamps (N) is 400. To find N/2:
N/2=400/2=200
We need to find the class interval where the cumulative frequency is greater than or equal to 200. From the cumulative frequency table, we see:
- The cumulative frequency just before 200 is 130 (for the class 2500 - 3000).
- The cumulative frequency that exceeds 200 is 216 (for the class 3000 - 3500).
For the median class (3000 - 3500):
- L (lower boundary of median class) = 3000
- F (frequency of median class) = 86
- CF (cumulative frequency of the class preceding the median class) = 130
- H (width of the median class) = 3500 - 3000 = 500
The formula for the median in a grouped frequency distribution is:
Median=L+(N/2−CFF)×H
Median=3000+(200−13086)×500
First, calculate N/2−CF:
N/2−CF=200−130=70
Median=3000+(7086)×500
7086≈0.813
0.813×500≈406.5
Median≈3000+406.5=3406.5
The median life of the neon lamps is approximately 3406.5 hours.
Topper's Solved these Questions
Similar Questions
The following table gives the distribution of the life time of 400 neon lamps Find the median life of a lamp.
View SolutionThe following table gives the life times of 400 neon lamps:
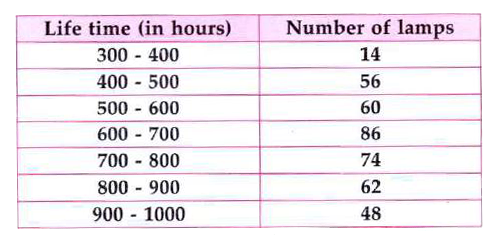
How many lamps have a life time of more than 700 hours?View SolutionThe following table gives the life times of 400 neon lamps:
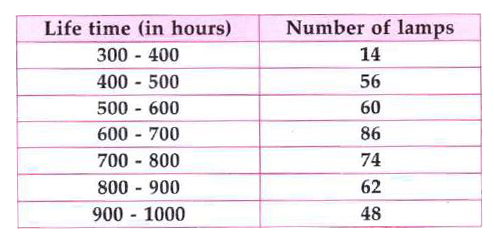
Represent the given information with the help of a histogram.View SolutionThe following table gives the life times of 400 neon lamps:(i) Represent the given information with the help of histogram.(ii) How many lamps have a life time of more than 700 hours?
View SolutionThe following table gives the life time of 400 neon lamps: Life time (in hours 300-400 400-500 500-600 600-700 700-800 800-900 900-1000 No. of lamps: 14 56 60 86 74 62 48 A bulb is selected at random. Find the probability that the life time of the selected bulb is : less than 400 between 300 to 800 hours at least 700 hours.
View SolutionAt present, a firm is manufacturing 2000 items. It is estimated that the rate of change of production P w.r.t. additional number of workers x is given by dPdx=100−12√x. If the firm employs 25 more workers, then the new level of production of items is (1) 3000 (2) 3500 (3) 4500 (4) 2500
View SolutionGopi Chand maintains his books of account on Single Entry System. Calculate his profit on 31st March, 2019 from the following information:
Liabilities and Assets1st April, 2018 (Rs.)31st March, 2019 (Rs.)Cash in Hand1,500500Bank Balance4,5003,500Fumiture2,0002,000Stock1,0003,000Creditors4,0003,000Debtors3,0004,000
During the year his drawings were Rs. 1,000 and additional capital invested Rs. 2,000.View SolutionEnter the following in the books of Karan, Delhi to close his accounts on 31st March, 2019. Pass the closing entries.
Opening Stock Rs. 20,000, Purchases Rs. 60,000, Wages Rs. 12,000, Salaries Rs. 16,000, Sales Rs. 88,000, Freight Inwards Rs. 4,000, Purchases Return Rs. 2,000, Sales Return Rs. 3,000, Carriage Outwards Rs. 2,500, Rent Rs. 3,000, Insurance Rs. 1,000, Discount Allowed Rs. 2,000, Discount Received Rs. 1,000, Repairs Rs. 1,000, Electricity Rs. 1,500, Commission Received Rs. 4,000, Interest on Investments Rs. 1,800, Interest (Dr.) 1,000, Closing Stock Rs. 40,000.View SolutionJournalise the following transaction in the Books of the M/s Bhanu Traders and Post them into the Ledger.
1. Started business with cash 92,000
2. Deposited into bank 60,000
4. Bought goods on credit from Himani 40,000
6. Purchased goods from cash 20,000
8. Returned goods to Himani 4,000
10. Sold goods for cash 20,000
14. Cheque given to Himani 36,000
17. Goods sold to M/s Goyal Traders. 3,50,000
19. Drew cash from bank for personal use 2,000
21. Goyal traders returned goods 3,500
22. Cash deposited into bank 20,000
26. Cheque received from Goyal Traders 31,500
28. Goods given as charity 2,000
29. Rent paid 3,000
30. Salary paid 7,000
31. Office machine purchased for cash 3,000View SolutionBank Statement of a customer shows bank balance of Rs. 62,000 on 31st March, 2019. On comparing it with the Cash Book the following discreption were noted
(i) Cheques were pain into the bank in March but were credited in Apirl: P-Rs. 3,500 ,Q -Rs. 2,500, R-Rs.2,000.
(ii) Cheques issued in March were presented in April , X-Rs. 4,000, Q-Rs. 4,500
(iii) Cheque for Rs. 1,000 received fromf customer entered in the Cash Book but was not banked.
(iv) Pass Book shows a debit of Rs. 1,000 for bank charges and credit of Rs. 2,000 as interest
(v) Intreste on investment Rs. 2,500 collected by the bank appeared in the Pass Book.
Prepare Bank Reconcilition Statement showing the balance as per Cash Book on 31st March, 2019.View Solution

