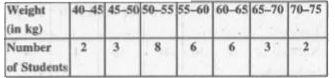
The distribution below gives the weight of 30 students in a class. Find the median weight of students: Weight (in kg): 40-45 45-50 50-55 55-60 60-65 65-70 70-75 No. of students: 2 3 8 6 6 3 2
To find the median weight of the students from the given distribution, we will follow these steps:
Step 1: Create a Cumulative Frequency Table
We start with the given data:
| Weight (in kg) | No. of Students |
|----------------|------------------|
| 40 - 45 | 2 |
| 45 - 50 | 3 |
| 50 - 55 | 8 |
| 55 - 60 | 6 |
| 60 - 65 | 6 |
| 65 - 70 | 3 |
| 70 - 75 | 2 |
Now, we calculate the cumulative frequency (CF):
- For the interval 40-45: CF = 2
- For the interval 45-50: CF = 2 + 3 = 5
- For the interval 50-55: CF = 5 + 8 = 13
- For the interval 55-60: CF = 13 + 6 = 19
- For the interval 60-65: CF = 19 + 6 = 25
- For the interval 65-70: CF = 25 + 3 = 28
- For the interval 70-75: CF = 28 + 2 = 30
The cumulative frequency table is:
| Weight (in kg) | No. of Students | Cumulative Frequency |
|----------------|------------------|----------------------|
| 40 - 45 | 2 | 2 |
| 45 - 50 | 3 | 5 |
| 50 - 55 | 8 | 13 |
| 55 - 60 | 6 | 19 |
| 60 - 65 | 6 | 25 |
| 65 - 70 | 3 | 28 |
| 70 - 75 | 2 | 30 |
Step 2: Determine the Median Class
The total number of students (n) = 30. To find the median, we calculate n/2:
n/2=30/2=15
Now we look for the cumulative frequency just greater than or equal to 15. From the table, we see that the cumulative frequency of 19 corresponds to the interval 55-60. Thus, the median class is 55-60.
Step 3: Apply the Median Formula
The formula for the median in a grouped frequency distribution is:
Median=l+(n/2−cff)×h
Where:
- l = lower boundary of the median class = 55
- n = total number of observations = 30
- cf = cumulative frequency of the class preceding the median class = 13 (for the class 50-55)
- f = frequency of the median class = 6 (for the class 55-60)
- h = width of the class intervals = 5 (since 55-60 is the interval)
Step 4: Substitute the Values
Now substituting the values into the formula:
Median=55+(15−136)×5
Calculating inside the parentheses:
=55+(26)×5
=55+(13)×5
=55+53
=55+1.67(approximately)
=56.67
Conclusion
The median weight of the students is approximately 56.67 kg.
---
We start with the given data:
|----------------|------------------|
| 40 - 45 | 2 |
| 45 - 50 | 3 |
| 50 - 55 | 8 |
| 55 - 60 | 6 |
| 60 - 65 | 6 |
| 65 - 70 | 3 |
| 70 - 75 | 2 |
- For the interval 45-50: CF = 2 + 3 = 5
- For the interval 50-55: CF = 5 + 8 = 13
- For the interval 55-60: CF = 13 + 6 = 19
- For the interval 60-65: CF = 19 + 6 = 25
- For the interval 65-70: CF = 25 + 3 = 28
- For the interval 70-75: CF = 28 + 2 = 30
|----------------|------------------|----------------------|
| 40 - 45 | 2 | 2 |
| 45 - 50 | 3 | 5 |
| 50 - 55 | 8 | 13 |
| 55 - 60 | 6 | 19 |
| 60 - 65 | 6 | 25 |
| 65 - 70 | 3 | 28 |
| 70 - 75 | 2 | 30 |
The total number of students (n) = 30. To find the median, we calculate n/2:
The formula for the median in a grouped frequency distribution is:
- l = lower boundary of the median class = 55
- n = total number of observations = 30
- cf = cumulative frequency of the class preceding the median class = 13 (for the class 50-55)
- f = frequency of the median class = 6 (for the class 55-60)
- h = width of the class intervals = 5 (since 55-60 is the interval)
Now substituting the values into the formula:
The median weight of the students is approximately 56.67 kg.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The weight of 10 students (in kg) are
55,40,35,52,60,38,36,45,31,44.
The median weight isA40 kgB41 kgC42 kgD44kgThe mean weight of 150 students in a class is 60 kg. the mean weight of boys is 70 kg and that of girls is 55 kg. What is the number of boys in the class?
A50B60C75D100The mean weight of 60 students of a class is 52.75 kg. If the mean weight of 25 of them is 51 kg., find the mean weight of remaining students.
A58 kgB56 kgC54 kgD51 kg
The weight (in kg) of students are given below :

Find the median weight of a student.
View SolutionFollowing is the data showing weights of 40 students in a class . Find its median .
View SolutionThe mean weight of 20 students is 25 kg and the mean weight of another 10 students in 40 kg . Find the mean weight of the 30 students .
View SolutionThe weights of 10 students ( in kilograms) are 36,45,31,52,35,40,55,60,38,44 Find the median weight
View SolutionThe average weight of 20 students in a class is increased by 0.75 kg when one of the students weighing 30 kg is replaced by a new student. Weight of the new student (in kg) is :
View Solution