The following table gives weekly wages in rupees of workers in a certain commercial organization. The frequency of class 49-52 is missing. It is known that the mean of the frequency distribution is 47.2. Find the missing frequency. Weekly wages (Rs.) 40-43 43-46 46-49 49-52 52-55 No. of workers: 31 58 60 ? 27
To find the missing frequency in the given frequency distribution, we will follow these steps:
Step 1: Set Up the Problem
We know the weekly wages and the corresponding frequencies, with the missing frequency for the class 49-52. We also know that the mean of the distribution is 47.2.
Step 2: Calculate the Midpoints (x_i)
The midpoints for each class interval can be calculated as follows:
- For 40-43: x1=40+432=41.5
- For 43-46: x2=43+462=44.5
- For 46-49: x3=46+492=47.5
- For 49-52: x4=49+522=50.5
- For 52-55: x5=52+552=53.5
Step 3: Create a Table
We will create a table with the midpoints, frequencies, and the deviations from the assumed mean (let's take the assumed mean A=47.5).
| Weekly Wages (Rs.) | Midpoint (x_i) | Frequency (f_i) | Deviation (d_i = x_i - A) | u_i = d_i / 3 |
|---------------------|----------------|------------------|---------------------------|----------------|
| 40-43 | 41.5 | 31 | 41.5 - 47.5 = -6 | -2 |
| 43-46 | 44.5 | 58 | 44.5 - 47.5 = -3 | -1 |
| 46-49 | 47.5 | 60 | 47.5 - 47.5 = 0 | 0 |
| 49-52 | 50.5 | f (missing) | 50.5 - 47.5 = 3 | 1 |
| 52-55 | 53.5 | 27 | 53.5 - 47.5 = 6 | 2 |
Step 4: Calculate the Summation of Frequencies
The total frequency is:
N=31+58+60+f+27=176+f
Step 5: Calculate the Summation of f_i * u_i
We calculate the products of frequencies and their corresponding u_i values:
- For 40-43: 31×−2=−62
- For 43-46: 58×−1=−58
- For 46-49: 60×0=0
- For 49-52: f×1=f
- For 52-55: 27×2=54
Thus, the summation is:
Σfiui=−62−58+0+f+54=−66+f
Step 6: Set Up the Mean Equation
Using the mean formula:
¯x=A+ΣfiuiN⋅h
Where h=3 (the width of the classes).
Substituting the known values:
47.2=47.5+−66+f176+f⋅3
Step 7: Solve for f
Rearranging gives:
−0.3=−66+f176+f⋅3
Multiplying both sides by 176+f:
−0.3(176+f)=3(−66+f)
Expanding both sides:
−52.8−0.3f=−198+3f
Bringing all terms involving f to one side:
−52.8+198=3f+0.3f
145.2=3.3f
Dividing by 3.3:
f=145.23.3≈44
Conclusion
The missing frequency f for the class 49-52 is 44.
---
We know the weekly wages and the corresponding frequencies, with the missing frequency for the class 49-52. We also know that the mean of the distribution is 47.2.
The midpoints for each class interval can be calculated as follows:
- For 40-43: x1=40+432=41.5
- For 43-46: x2=43+462=44.5
- For 46-49: x3=46+492=47.5
- For 49-52: x4=49+522=50.5
- For 52-55: x5=52+552=53.5
We will create a table with the midpoints, frequencies, and the deviations from the assumed mean (let's take the assumed mean A=47.5).
|---------------------|----------------|------------------|---------------------------|----------------|
| 40-43 | 41.5 | 31 | 41.5 - 47.5 = -6 | -2 |
| 43-46 | 44.5 | 58 | 44.5 - 47.5 = -3 | -1 |
| 46-49 | 47.5 | 60 | 47.5 - 47.5 = 0 | 0 |
| 49-52 | 50.5 | f (missing) | 50.5 - 47.5 = 3 | 1 |
| 52-55 | 53.5 | 27 | 53.5 - 47.5 = 6 | 2 |
The total frequency is:
N=31+58+60+f+27=176+f
We calculate the products of frequencies and their corresponding u_i values:
- For 40-43: 31×−2=−62
- For 43-46: 58×−1=−58
- For 46-49: 60×0=0
- For 49-52: f×1=f
- For 52-55: 27×2=54
Σfiui=−62−58+0+f+54=−66+f
Using the mean formula:
¯x=A+ΣfiuiN⋅h
Where h=3 (the width of the classes).
47.2=47.5+−66+f176+f⋅3
Rearranging gives:
−0.3=−66+f176+f⋅3
Multiplying both sides by 176+f:
−0.3(176+f)=3(−66+f)
Expanding both sides:
−52.8−0.3f=−198+3f
Bringing all terms involving f to one side:
−52.8+198=3f+0.3f
145.2=3.3f
Dividing by 3.3:
f=145.23.3≈44
The missing frequency f for the class 49-52 is 44.
Topper's Solved these Questions
Similar Questions
The mean of the following distribution is 52 and the frequency of class interval 30-40 is f. Find f.
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
View SolutionThe mean of the following frequency distribution is 50, but the frequencies f1andf2 in class 20-40 and 60-80 respectively are not known. Find these frequencies.

Given that the sum of frequencies is 120.View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x), 0, 1 , 2 , 3, 4, 5 , Total Frequency is 200 and no. of days (f): 46 , ? , ? , 25 , 10 , 5
View SolutionIf the median of the following frequency distribution is 46, find the missing frequencies. Variable: 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Total Frequency: 12 30 ? 65 ? 25 18 230
View SolutionIf the median of the following frequency distribution is 28.5 find the missing frequencies: Class interval: 0-10 10-20 20-30 30-40 40-50 50-60 Total Frequency: 5 f1 20 15 f2 5 60
View SolutionThe following table gives the weekly wages of workers in a factory. Weekly wages(Rs) 50-55 55-60 60-65 65-70 70-75 75-80 80-85 85-90 No. of workers 5 20 10 10 9 6 12 18 Calculate the mean, by using Short Cut Method.
View SolutionThe mean of the following distribution is 50 but the frequency f1andf2 in classes 20-40 and 60-80, resepectively are not known. Find these frequencies, if the sum of all the fequencies is 120
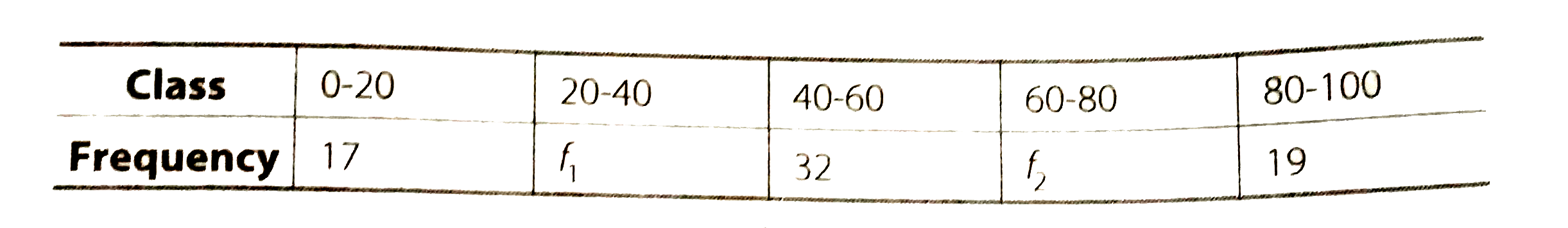 View Solution
View SolutionFind the median of the following frequency distribution: Weekly wages (in Rs.) 60-69 70-79 80-89 90-99 100-109 110-119 No. of days: 5 15 20 30 20 8
View Solution

