The following table shows the ages of the patients admitted in a hospital during a year:Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
To solve the problem, we need to find the mode and the mean of the ages of patients admitted to the hospital. Let's break this down step by step.
Step 1: Organize the Data
We have the following age groups and their corresponding frequencies:
| Age Group (Years) | Frequency (Fi) |
|-------------------|----------------|
| 5 - 15 | 6 |
| 15 - 25 | 11 |
| 25 - 35 | 21 |
| 35 - 45 | 23 |
| 45 - 55 | 14 |
| 55 - 65 | 5 |
Step 2: Calculate the Mean
To calculate the mean, we first need to find the mid-point (Xi) for each age group and then calculate Fi * Xi.
1. Calculate Mid-point (Xi):
- For 5 - 15: (5 + 15) / 2 = 10
- For 15 - 25: (15 + 25) / 2 = 20
- For 25 - 35: (25 + 35) / 2 = 30
- For 35 - 45: (35 + 45) / 2 = 40
- For 45 - 55: (45 + 55) / 2 = 50
- For 55 - 65: (55 + 65) / 2 = 60
| Age Group (Years) | Frequency (Fi) | Mid-point (Xi) | Fi * Xi |
|-------------------|----------------|-----------------|---------|
| 5 - 15 | 6 | 10 | 60 |
| 15 - 25 | 11 | 20 | 220 |
| 25 - 35 | 21 | 30 | 630 |
| 35 - 45 | 23 | 40 | 920 |
| 45 - 55 | 14 | 50 | 700 |
| 55 - 65 | 5 | 60 | 300 |
| Total | 80 | | 2830|
2. Calculate the Mean:
Mean=∑(Fi⋅Xi)∑Fi=283080=35.375
Step 3: Calculate the Mode
To find the mode, we need to identify the modal class, which is the class with the highest frequency.
- The highest frequency is 23, which corresponds to the age group 35 - 45.
Using the mode formula:
Mode=L+f1−f0(2f1−f0−f2)⋅h
Where:
- L = lower limit of the modal class = 35
- f1 = frequency of the modal class = 23
- f0 = frequency of the class before the modal class = 21
- f2 = frequency of the class after the modal class = 14
- h = width of the class interval = 10
Substituting the values:
Mode=35+23−21(2⋅23−21−14)⋅10
=35+2(46−21−14)⋅10
=35+211⋅10
=35+2011≈36.818
Step 4: Compare and Interpret the Two Measures of Central Tendency
- Mean: 35.375
- Mode: 36.818
Interpretation:
- The mean age of patients is approximately 35.38 years, while the mode age is approximately 36.82 years.
- The mode indicates that the most common age group of patients admitted is around 36.82 years, while the mean provides an average that is slightly lower, suggesting that there are some younger patients that pull the average down.
- This comparison shows that while the average age is lower, the most frequently occurring age is slightly higher, indicating a concentration of patients around that age.
We have the following age groups and their corresponding frequencies:
|-------------------|----------------|
| 5 - 15 | 6 |
| 15 - 25 | 11 |
| 25 - 35 | 21 |
| 35 - 45 | 23 |
| 45 - 55 | 14 |
| 55 - 65 | 5 |
To calculate the mean, we first need to find the mid-point (Xi) for each age group and then calculate Fi * Xi.
- For 5 - 15: (5 + 15) / 2 = 10
- For 15 - 25: (15 + 25) / 2 = 20
- For 25 - 35: (25 + 35) / 2 = 30
- For 35 - 45: (35 + 45) / 2 = 40
- For 45 - 55: (45 + 55) / 2 = 50
- For 55 - 65: (55 + 65) / 2 = 60
|-------------------|----------------|-----------------|---------|
| 5 - 15 | 6 | 10 | 60 |
| 15 - 25 | 11 | 20 | 220 |
| 25 - 35 | 21 | 30 | 630 |
| 35 - 45 | 23 | 40 | 920 |
| 45 - 55 | 14 | 50 | 700 |
| 55 - 65 | 5 | 60 | 300 |
| Total | 80 | | 2830|
Mean=∑(Fi⋅Xi)∑Fi=283080=35.375
To find the mode, we need to identify the modal class, which is the class with the highest frequency.
Mode=L+f1−f0(2f1−f0−f2)⋅h
Where:
- L = lower limit of the modal class = 35
- f1 = frequency of the modal class = 23
- f0 = frequency of the class before the modal class = 21
- f2 = frequency of the class after the modal class = 14
- h = width of the class interval = 10
Mode=35+23−21(2⋅23−21−14)⋅10
=35+2(46−21−14)⋅10
=35+211⋅10
=35+2011≈36.818
- Mean: 35.375
- Mode: 36.818
- The mean age of patients is approximately 35.38 years, while the mode age is approximately 36.82 years.
- The mode indicates that the most common age group of patients admitted is around 36.82 years, while the mean provides an average that is slightly lower, suggesting that there are some younger patients that pull the average down.
- This comparison shows that while the average age is lower, the most frequently occurring age is slightly higher, indicating a concentration of patients around that age.
Similar Questions
The following table shows the ages of the patients admitted in a hospital during a year: Age (in years): 5-15 15-25 25-35 35-45 45-55 55-65 No. of students: 6 11 21 23 14 5 Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
View SolutionThe following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret, the two measures: Number of students per Teacher Number of States/U.T. 15-20 3 20-25 8 25-30 9 30-35 10 35-40 3 40-45 0 45-50 0 50-55 2
View SolutionThe data on the number of patients attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.
 View Solution
View SolutionThe following table given the daily income of 50 workers of a factory :

Find the mean of above data.View SolutionThe following graph show the temprature of a patient in a hospital, recorded every hour, (a) What was the patient's temperature at 1 p.m.? *b) When was the patient's temperature 38.5∘C ? (c) The patient’s temperature was the same two times during the period given. What were these two times? (d) What was the temperature at 1.30 p.m.? How did you arrive at your answer? (e) During which periods did the patients’ temperature showed an upward trend?
View SolutionA die is thrown 12 times and the source are recorded in the following table.

Find the range, mean and mode of the given scores.View SolutionThe data on the number of patient attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.
Take the assumed mean as 45. Give your answer correct to 2 decimal places.
 View Solution
View SolutionFollowing table shows the number of bicycles manufactured in a factory during the years 1998 to 2002. Illustrate this data using a bar graph. Choose a scale of your choice
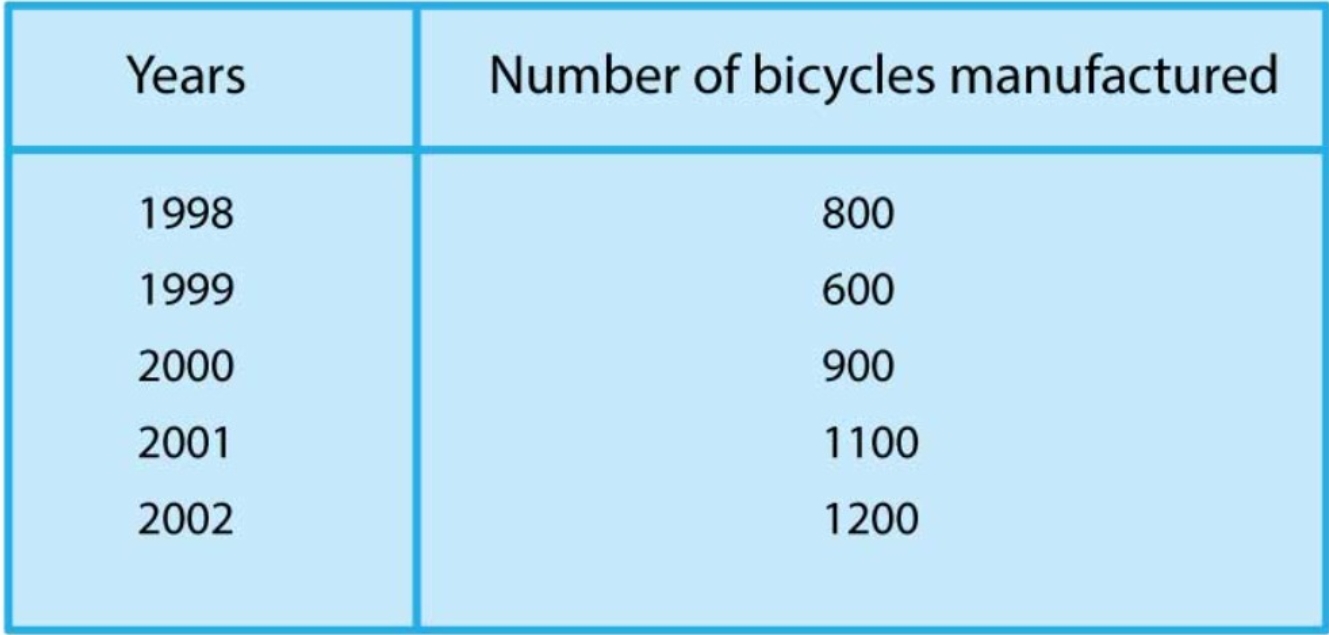 View Solution
View SolutionThe age of 40 student of a class is given in the following table. Find their mean short cut method:
 View Solution
View SolutionThe following table shows the weights of 12 persons.
Weight (in kg): 48 50 52 54 58
Number of persons: 4 3 2 2 1
Find the median and mean weights. Using empirical relation, calculate its mode.View Solution

