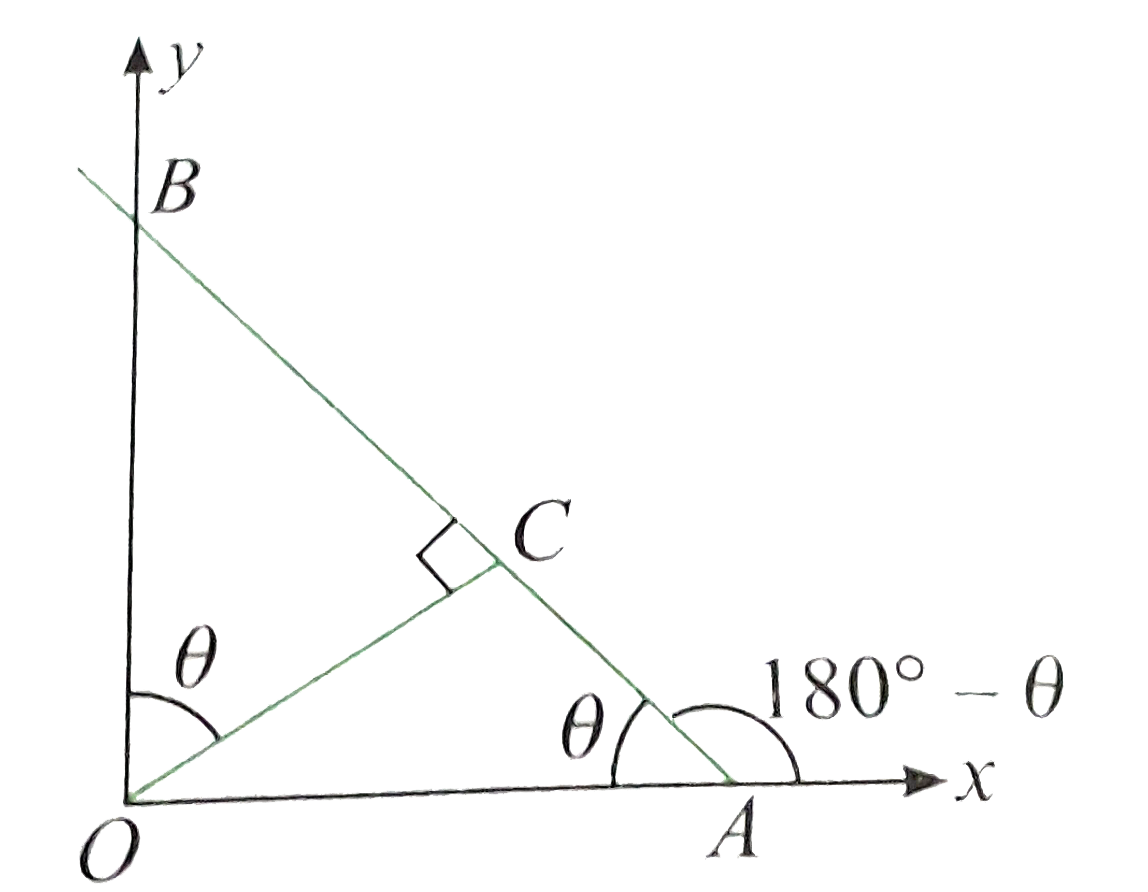
The foot of the perpendicular on the line 3x+y=λ drawn from the origin is C. If the line cuts the x and the y-axis at AandB , respectively, then BC:CA is
1:3
3:1
1:9
9:1
The correct Answer is:D
tan180∘−θ)=Slope of AB=−3
∴tanθ=3
∴OCAC=tanθ,OCBC=cotθ
or BCAC=tanθcotθ=tan2θ=9
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct13videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Linked10videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.69videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0.
View SolutionFind the equation of the line perpendicular to the line xa−yb=1 and passing through a point at which it cuts the x-axis.
View SolutionFind the equation of the line perpendicular to the line xa−yb=1 and passing through a point at which it cuts the x-axis.
View SolutionFind the co-ordinates of the foot of perpendicular drawn from the point (3,−3) to the line x−2y=4.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point (2,3) to the line y=3x+4
View SolutionThe perpendicular drawn from origin to the line y=mx+c meets the line at point (−1,−2), (c,m)=?
View SolutionA line L varies such that length of perpendicular on it from origin O is always 4 units. If L cuts x-axis and y-axis at A and B respectively then minimum value of (OA)2+(OB)2 is
View SolutionFind the coordinates of the foot of perpendicular drawn from origin to the planes: 2x−3y+4z−6=0
View SolutionThe co-ordinates of the foot of perpendicular drawn from origin to a line are (2,3). Find the equation of the line.
View Solution

