The function f(x)=e−|x| is
A
continuous everywhere but not differentiable at x=0
B
continuous and differentiable everywhere
C
not continuous at x=0
D
None of above
Video Solution
Text Solution
The correct Answer is:A
It is clear from the figure that f(x) is continuous everywhere and not differetiable at x=0 due to sharp edge.
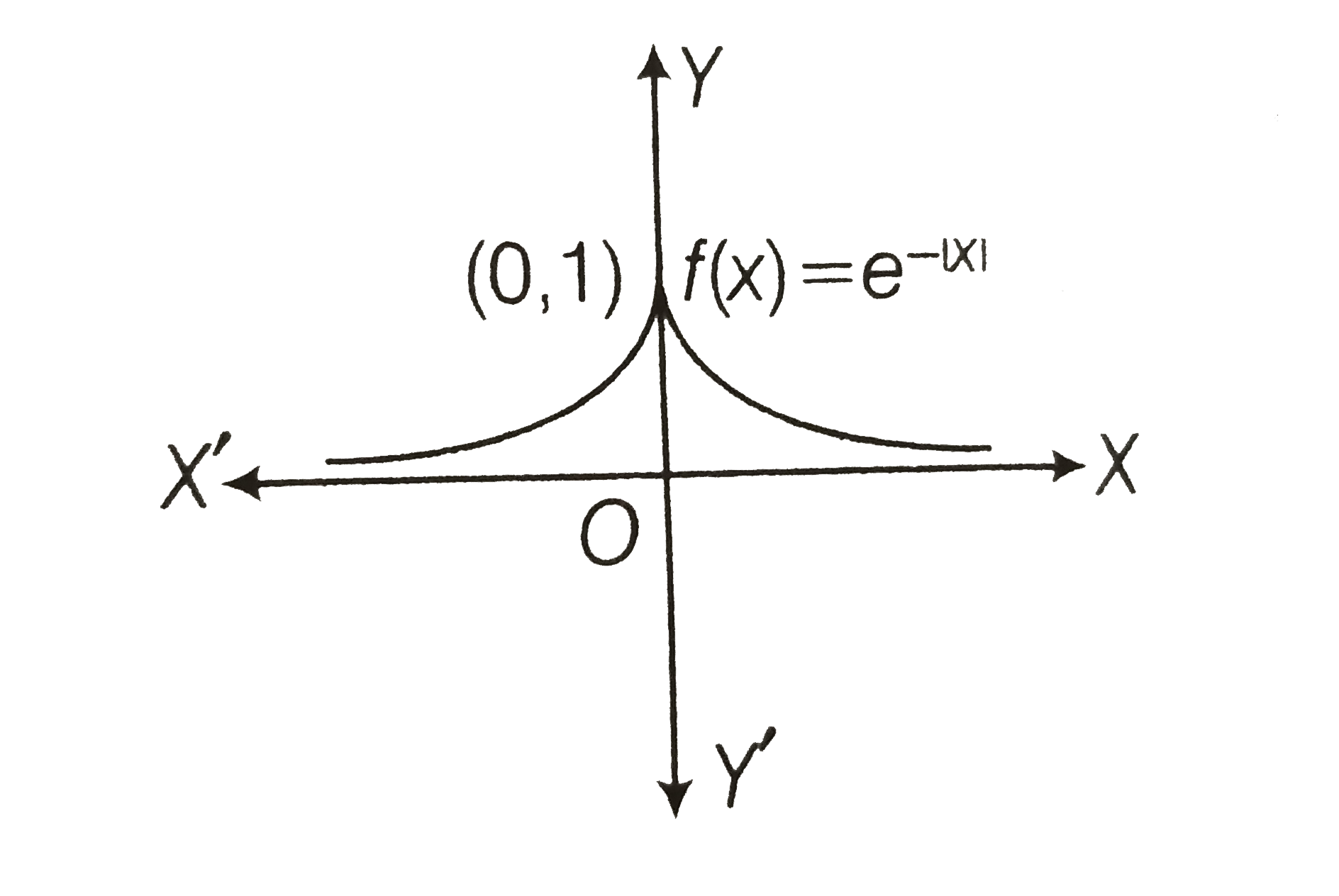
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The interval in which the function f(x)=(x+2)e−x is decreasing in
A(−1,∞)B(-1,1)C(-1,2)D(1,2)Consider the following statements:
1. The function f(x)=|x| is not differentiable at x=1.
2. The function f(x)=ex is not differentiable at x=0.
Which of the above statements is/are correct ?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2Consider the following statements:
I. The function f(x)=|x| is not differentiable at x = 1
II. The function f(x)=ex is differentiable at x = 0
Which of the above statements is/are correct?AOnly IBOnly IICBoth I nor IIDNeither I nor II
The function f(x)=x2 e−x is monotonic increasing when (a) x∈R−[0, 2] (b) 0<x<2 (c) 2<x<∞ (d) x<0
View SolutionThe interval in which the function f(x)=x2e−x is non-decreasing, is
View SolutionThe range of the function f(x)=ex−e−x is
View SolutionShow that the function f(x)=ex is strictly increasing on R.
View SolutionThe function f(x)=xe1−x stricly
View Solution
