The given figure is made up of a large circle PQRST with centre O and diameter 28 cm, a small circle QAOB, two semi-circles and a sector OST. Find the total shaded area of the figure.
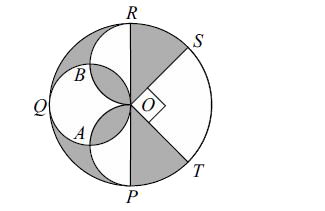
(198π−98)cm2
(49π+198)cm2
(150π+100)cm2
(147π–196)cm2
The correct Answer is:D
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET BEXERCISE - EVERYDAY MATHEMATICS10videos
IMO QUESTION PAPER 2019 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET AEXERCISE - Achievers section5videos
IMO QUESTION PAPER 2019 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2020 SET 1
Similar Questions
In the given figure, O is the centre of the circle.

Shade sectors OAC and OPB.View SolutionIn given figure, O is the centre of the circle.
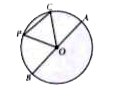
A chord, which is not the diameter of the circle isView SolutionIn the given figure OABC is a quadrant of a circle with centre O and radius 3.5cm.If OD=2cm,find the area of the shaded region.
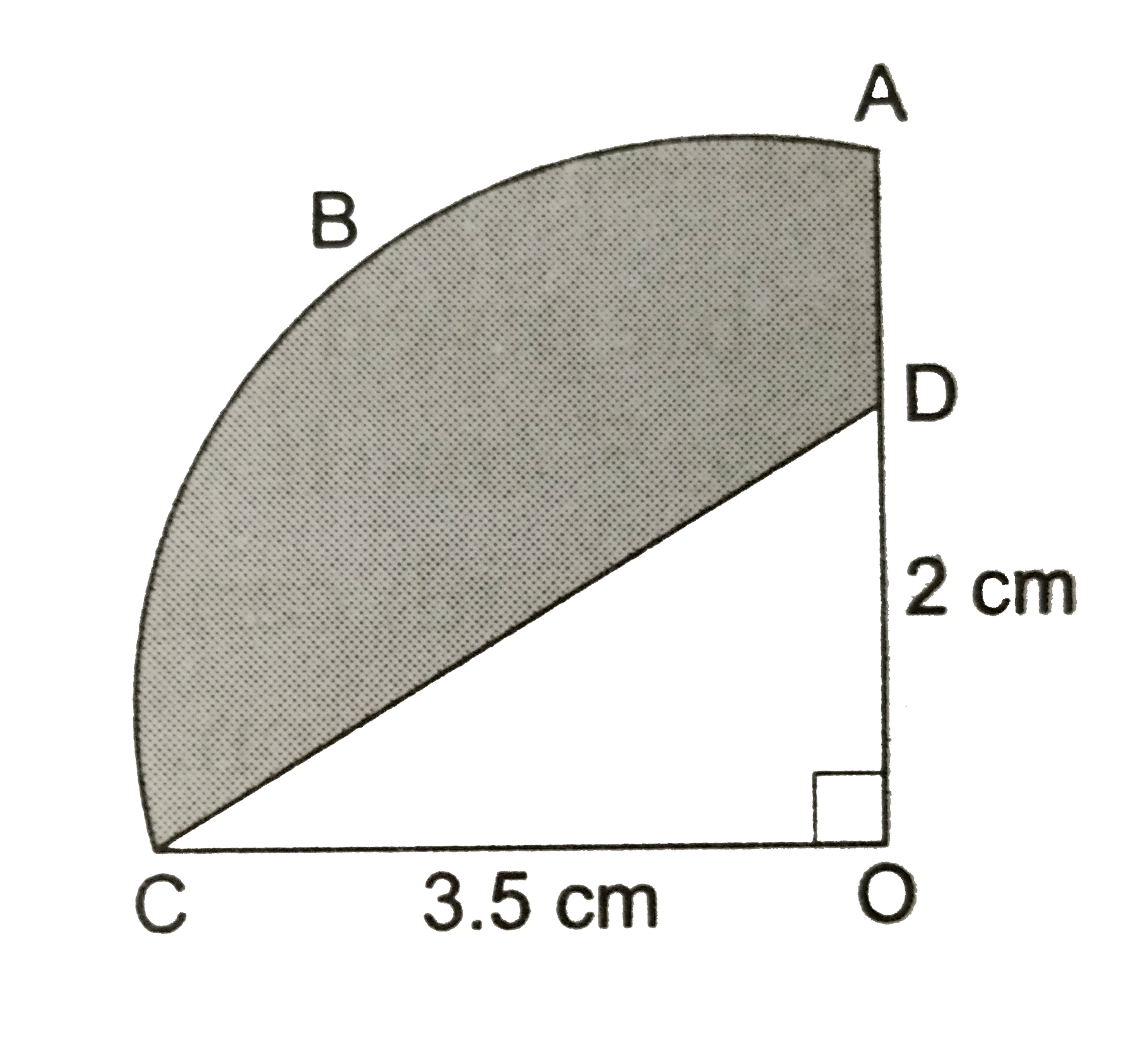 View Solution
View SolutionIn figure, OACB is a quadrant of a circle with centre O and radius 7 cm. If AD = 2 cm, find the area of the shaded region.
 View Solution
View SolutionIn the given figure, O is the centre of the circle.

Name a chord, which is not the diameter of the circle.View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
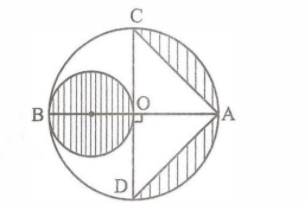 View Solution
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn the given figure,diameter of larger semi-circle is 14 cm and radius of smaller semi-circle is 3.5cm. find :
View Solution

