The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.
To prove that point F is equidistant from lines AB and AC in triangle ABC where AD bisects angle BAC and EG is the perpendicular bisector of side AB intersecting AD at point F, we can follow these steps:
Step 1: Identify the triangles
Consider triangles AFE and AFL. Here, point F lies on AD, and EG is the perpendicular bisector of AB.
Step 2: Establish right angles
Since EG is the perpendicular bisector of AB, we know that:
- Angle AFE = 90° (because EG is perpendicular to AB)
- Angle AFL = 90° (because EG is perpendicular to AB)
Step 3: Use the angle bisector property
Since AD bisects angle BAC, we have:
- Angle LAF = Angle FAE
Step 4: Identify the common side
Both triangles AFE and AFL share a common side:
- AF = AF (common side)
Step 5: Apply the criteria for triangle congruence
Now we can use the Angle-Angle-Side (AAS) criterion for triangle congruence:
- Triangle AFE is congruent to triangle AFL.
Step 6: Conclude using CPCTC
Since triangles AFE and AFL are congruent, by the Corresponding Parts of Congruent Triangles are Congruent (CPCTC) property:
- FE = AL
Step 7: Interpret the result
The equality FE = AL implies that point F is equidistant from lines AB and AC, as the segments FE and AL are perpendicular distances from point F to lines AB and AC, respectively.
Final Conclusion
Thus, we have proved that point F is equidistant from lines AB and AC.
---
Consider triangles AFE and AFL. Here, point F lies on AD, and EG is the perpendicular bisector of AB.
Since EG is the perpendicular bisector of AB, we know that:
- Angle AFE = 90° (because EG is perpendicular to AB)
- Angle AFL = 90° (because EG is perpendicular to AB)
Since AD bisects angle BAC, we have:
- Angle LAF = Angle FAE
Both triangles AFE and AFL share a common side:
- AF = AF (common side)
Now we can use the Angle-Angle-Side (AAS) criterion for triangle congruence:
- Triangle AFE is congruent to triangle AFL.
Since triangles AFE and AFL are congruent, by the Corresponding Parts of Congruent Triangles are Congruent (CPCTC) property:
- FE = AL
The equality FE = AL implies that point F is equidistant from lines AB and AC, as the segments FE and AL are perpendicular distances from point F to lines AB and AC, respectively.
Thus, we have proved that point F is equidistant from lines AB and AC.
Topper's Solved these Questions
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
- MATHEMATICS -2014BOOK - ICSECHAPTER - MATHEMATICS -2014EXERCISE - SECTION- B
29 Videos
Similar Questions
In triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
E is equidistant from A and B
View SolutionABC is an equilateral triangle .If AD bisects angle A, Prove that AD is perpendicular bisector of BC .
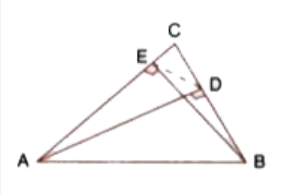
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
ΔABC~ΔDEC
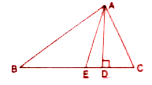
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that : point P is equidistant from A and B.
View SolutionThe given figure shows a triangle ABC, in which AB > AC. E is the mid-point of BC and AD is perpendicular to BC.
Prove that : AB2+AC2=2BE2+2AE2
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that :
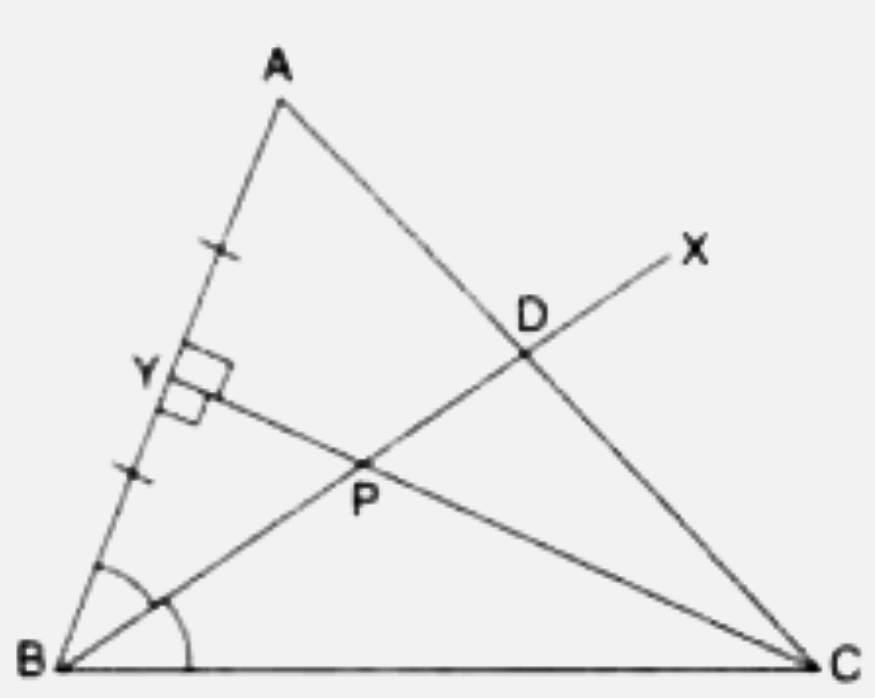
point D is equidistant from AB and BC.
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CD×AB=CA×DE
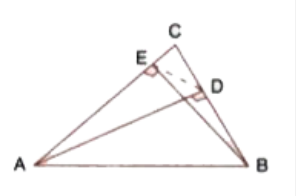
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
ΔADC~ΔBEC

View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
View Solution
