ABC is an equilateral triangle .If AD bisects angle A, Prove that AD is perpendicular bisector of BC .
The correct Answer is:x=24∘andy=54∘
To prove that AD is the perpendicular bisector of BC in an equilateral triangle ABC where AD bisects angle A, we will follow these steps:
Step 1: Understand the properties of an equilateral triangle
In an equilateral triangle, all sides are equal, and all angles are equal to 60 degrees.
Step 2: Identify the angles
Since AD bisects angle A, we have:
∠BAD=∠DAC
Step 3: Establish congruence of triangles
Consider triangles ABD and ACD. We know:
- AB=AC (sides of the equilateral triangle are equal)
- AD is common to both triangles
- ∠BAD=∠DAC (since AD bisects angle A)
By the Side-Angle-Side (SAS) congruence criterion, we can conclude:
△ABD≅△ACD
Step 4: Conclude properties from congruence
Since the triangles are congruent, we have:
- BD=DC (corresponding parts of congruent triangles are equal)
This shows that D is the midpoint of BC, hence AD bisects BC.
Step 5: Show that AD is perpendicular to BC
From the congruence of triangles ABD and ACD, we also have:
∠ADB=∠ADC
Since these two angles form a linear pair (they are adjacent angles on a straight line), we can write:
∠ADB+∠ADC=180∘
Let ∠ADB=∠ADC=x. Then:
x+x=180∘
2x=180∘
x=90∘
Thus, ∠ADB=90∘, which means AD is perpendicular to BC.
Conclusion
We have shown that AD is both the bisector of BC and perpendicular to it, proving that AD is the perpendicular bisector of BC.
---
In an equilateral triangle, all sides are equal, and all angles are equal to 60 degrees.
Since AD bisects angle A, we have:
∠BAD=∠DAC
Consider triangles ABD and ACD. We know:
- AB=AC (sides of the equilateral triangle are equal)
- AD is common to both triangles
- ∠BAD=∠DAC (since AD bisects angle A)
△ABD≅△ACD
Since the triangles are congruent, we have:
- BD=DC (corresponding parts of congruent triangles are equal)
From the congruence of triangles ABD and ACD, we also have:
∠ADB=∠ADC
∠ADB+∠ADC=180∘
x+x=180∘
2x=180∘
x=90∘
We have shown that AD is both the bisector of BC and perpendicular to it, proving that AD is the perpendicular bisector of BC.
Topper's Solved these Questions
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - INEQUALITIES
5 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - MID-POINT THEOREM
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - TRIANGLES
6 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
Similar Questions
InΔABC,AB=ACandD is a piont in side BC such that AD bisect angle BAC.
Show that AD is perpendicular bisector of side BC.
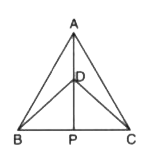
View SolutionThe given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that:
ΔABD=ΔACD
(ii) ΔABP=ΔACP
(iii) AP bisects ∠BDC
(iv) AP is perpendicular bisector of BC.
View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
View SolutionThe given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.
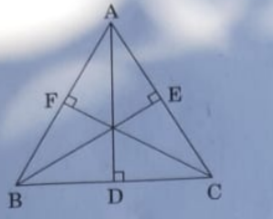
View SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
View SolutionTriangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : ABPQ=ADPM
View SolutionThe given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
Does the perpendicular bisector of BC pass through O?
View SolutionABC is a triangle. D is the middle point of BC. If AD is perpendicular to AC, The value of cos A cos C , is
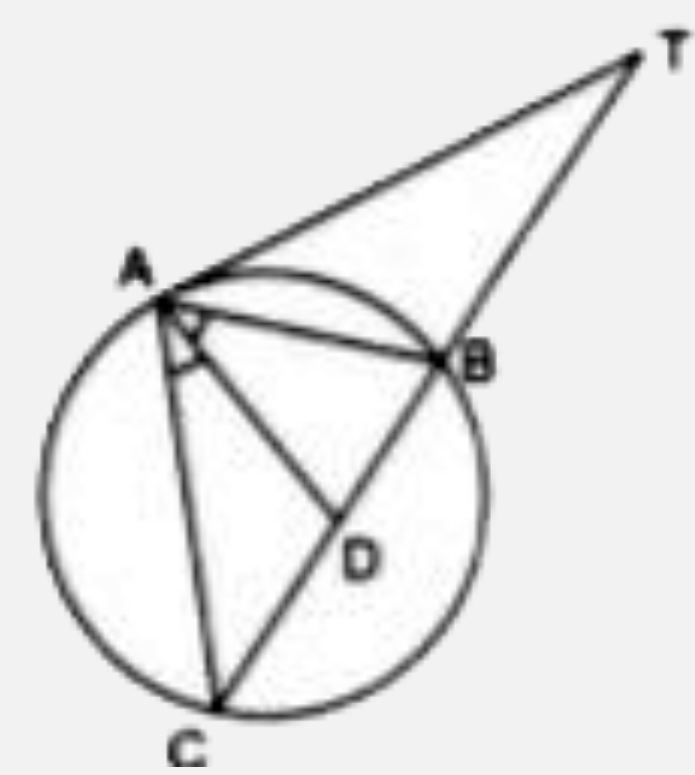
View SolutionIn the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
View Solution