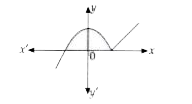
The graph of a polynomial p(x) cuts the x-axis at two places and touches it at the three places. Find the number of zeroes of p(x).
To find the number of zeroes of the polynomial p(x), we can follow these steps:
Step 1: Understand the behavior of the polynomial at the x-axis
The graph of a polynomial can either cut the x-axis or touch it. When the graph cuts the x-axis, it indicates that there is a root (zero) at that point. When it touches the x-axis, it indicates that there is a repeated root (zero) at that point.
Step 2: Count the cuts and touches
From the problem, we know:
- The polynomial cuts the x-axis at 2 places.
- The polynomial touches the x-axis at 3 places.
Step 3: Determine the contribution to the total number of zeroes
- Each cut contributes 1 zero.
- Each touch contributes 2 zeros (since it is a repeated root).
Step 4: Calculate the total number of zeroes
Using the information:
- Number of zeroes from cuts: 2 (since it cuts the x-axis at 2 places)
- Number of zeroes from touches: 3×2=6 (since it touches the x-axis at 3 places)
Now, we can add these contributions together:
Total number of zeroes=Zeroes from cuts+Zeroes from touches=2+6=8
Final Answer
The polynomial p(x) has a total of 8 zeroes.
---
The graph of a polynomial can either cut the x-axis or touch it. When the graph cuts the x-axis, it indicates that there is a root (zero) at that point. When it touches the x-axis, it indicates that there is a repeated root (zero) at that point.
From the problem, we know:
- The polynomial cuts the x-axis at 2 places.
- The polynomial touches the x-axis at 3 places.
- Each cut contributes 1 zero.
- Each touch contributes 2 zeros (since it is a repeated root).
Using the information:
- Number of zeroes from cuts: 2 (since it cuts the x-axis at 2 places)
- Number of zeroes from touches: 3×2=6 (since it touches the x-axis at 3 places)
Total number of zeroes=Zeroes from cuts+Zeroes from touches=2+6=8
The polynomial p(x) has a total of 8 zeroes.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - POLYNOMIALSEXERCISE - Olympiad/HOTS Corner15videos
POLYNOMIALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - POLYNOMIALSEXERCISE - EXERCISE (Subjective Problems) (Long Answer Type)4videos
POLYNOMIALS
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - NCERT SECTION (EXERCISE 3.7)18videos
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - Olympiad/HOTS Corner26videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
Zero of the polynomial p(x)=2x+5 is
A−25B−52C25D52 - Question 2 - Select One
Zero of the polynomial p(x)=2x+5 is
A−25B−52C25D52 - Question 3 - Select One
The zeros of the polynomial p(x)=x2−3x are
A0 , 0B0 , 3C0 , -3D3 , -3
The zeroes of the polynomial p(x)=x2−3x are
View Solution.The zeroes of the polynomial P(x)=x2−3x is
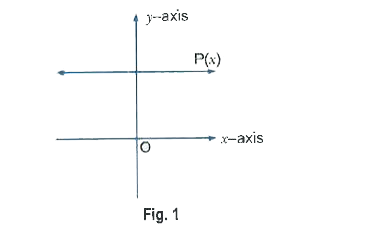
View SolutionGraph of polynomial P(x) is given below. Find the number of zeros of P(x)
 View Solution
View SolutionThe zeros of the polynomial p(x)=3x2−1 are
View SolutionThe zeros of the polynomial p(x)=x2+x−6 are
View Solution