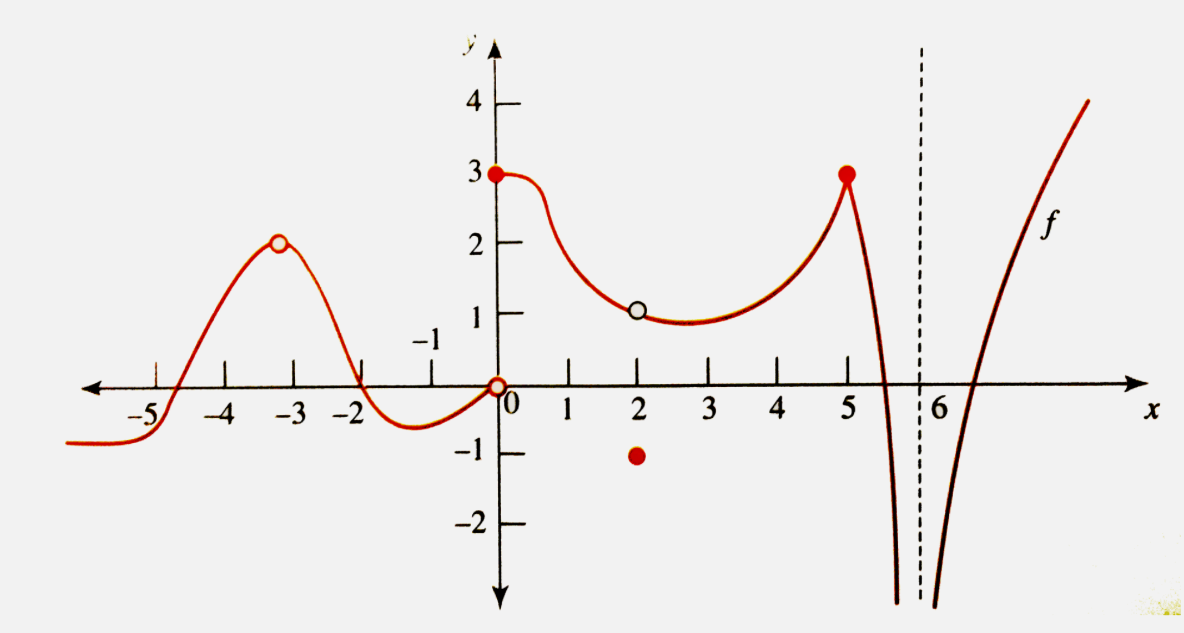
The graph of y=f(x) is as shown in the following figure.
(##CEN_GRA_C01_S01_016_Q01.png" width="80%">
Identify the points of discontinuity and give the reason for the same.

Text Solution
Verified by Experts

y = f(x) is discontinuous at x =- 3 as the value of the function is missing at this point. Assigning proper value to f(-3) [from the graph f(-3) = 2], f(x) can be made continuous at this point.
y = f(x) is discontinuous at x = 0 as there is a jump in the value of the function at this point. Here limx→0−f(x)andlimx→0+f(x)=3. At this point, the function cannot be made continuous.
At x = 2, the function is discontinuous as the value of the value of the function is not same as the limiting value of function.
That is, limx→2f(x)=1 (limit of the function exists), but f(2) =- 1.
At x = 6, the function is discontinuous as the value of the function is decreasing indefinitely when x is approached from either its left or its right.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSFUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In figure ,PR = ?
    (##CEN_JEE_MAT_X_C14_E01_032_Q01.png" width="80%">

    A20 cm
    B22 cm
    C24 cm
    D26 cm

  • In the figure shown
    (##AHT_PGT_PHY_C10_E01_006_Q01.png" width="80%">

    AP>P0
    BP<P0
    CP=P0
    DP=0

  • Match the following ( ##AAK_MCP_10_NEET_BOT_E10_027_Q01.png" width="80%">

    Aa(iv), b(v), c(ii), d(i), e(iii)
    Ba(v), b(iv), c(iii), d(ii), e(i)
    Ca(iv), b(v), c(i), d(ii), e(iii)
    Da(iv), b(v), c(ii), d(iii), e(i)