The growth of a quantity N(t) at any instant t is given by dN(t)dt=αN(t) , Given that N(t)=cekt , is constant. What is the value of α ?
c
k
c+k
c-k
The correct Answer is:B
To find the value of α in the differential equation given by
dN(t)dt=αN(t)
where N(t)=cekt (with c being a constant), we will follow these steps:
Step 1: Differentiate N(t)
First, we need to differentiate N(t)=cekt with respect to t.
dN(t)dt=ddt(cekt)
Using the chain rule, we get:
dN(t)dt=c⋅kekt
Step 2: Substitute N(t) into the differential equation
Now, we substitute N(t) into the original differential equation:
dN(t)dt=αN(t)
Substituting N(t):
c⋅kekt=α(cekt)
Step 3: Simplify the equation
We can simplify the equation by dividing both sides by cekt (assuming c≠0 and ekt≠0):
k=α
Conclusion
Thus, we find that:
α=k
Topper's Solved these Questions
Similar Questions
In the given circuit, the switch S is closed at time t = 0 . The charge Q on the capacitor at any instant t is given by Q(t)=Q(1−e−αt). Find the value of Q0 and α in terms of given parameters as shown in the circuit.
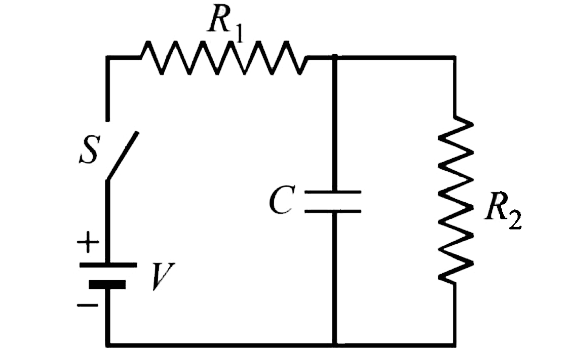 .
.
View SolutionPosition of a body with acceletation a is given box x=kamtn, where t is time and k is numeric constant. Find the value of m.
View Solution
Knowledge Check
The growth of a quantity N (t) at any constant t is given by dN(t)dt=αN(t) . Given that N (t) = cekt.c is a constant . What is the value of α ?
AcBkCc+kDc−kTwo right circular cylinders of equal volume have their heights in the ratio 1:2. The ratio of their radii is :
AcBkCc+kDc−kTime dependence of a physical quantity P is given by P=P0exp(−αt2), where α is a constant and t is time. The constant α is
AdimensionlessBhasdimensionsT−2Chas dimensions of P.DhasdimensionsT2
Given that s=t2+2t+3. Find dsdt.
View SolutionTime dependence of a physical quantity P is given by P=P0exp(−αt2), where α is a constant and t is time. The constant α is
View SolutionThe time dependence of a physical quantity P is given by P=P0exp(−αt2), where α is a constant and t is time. The constant α
View SolutionThe time dependence of a physical quantity P is given by P=P0 exp(−αt2), where α is a constant and t is time. The constant α
View SolutionThe flux linked with a coil at any instant 't' is given by ϕ=10t2−50t+250
The induced emf at t=3s is
View Solution
