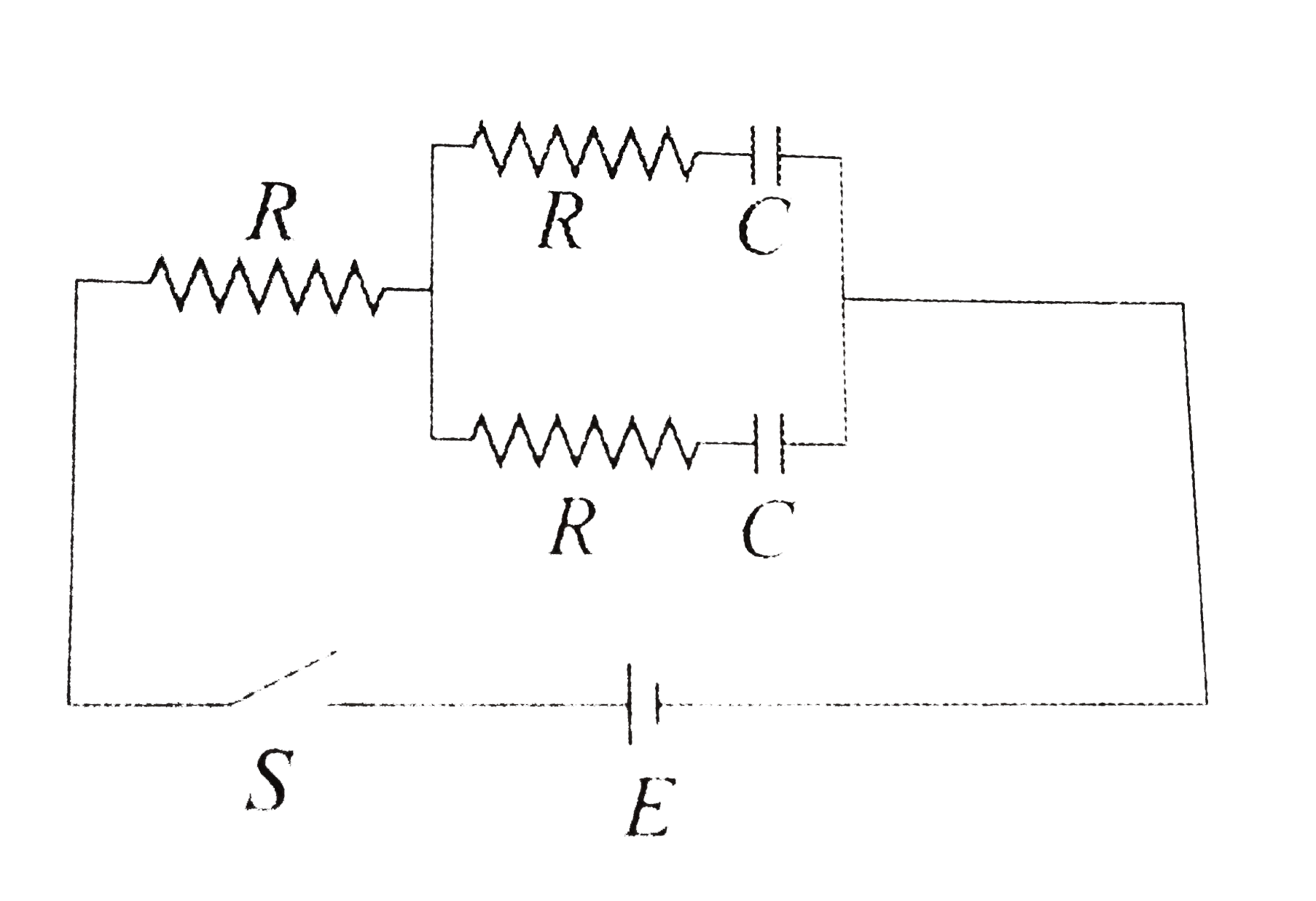
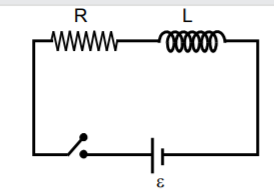
In the given circuit, the switch S is closed at time t = 0 . The charge Q on the capacitor at any instant t is given by Q(t)=Q(1−e−αt). Find the value of Q0 and α in terms of given parameters as shown in the circuit.
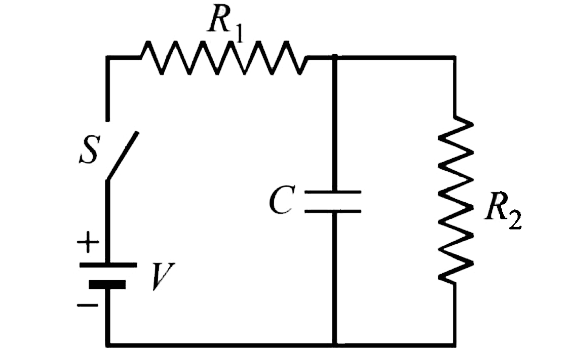 .
.
Video Solution
Text Solution
The correct Answer is:A, B, C
Given Q=Q0[1−eαt]
Here Q0=Maξμmchar≥and<br>alpha = 1/(tau_c) = 1/(C_(Req))<br>Nowthemaxiμmchar≥<br>Q_0 = C[V_(0)]whereV_0=maxpotentiald⇔erenceacrossC<br>= C[V/(R_1+R_2) xx R_2]<br>andtau_c = C R_(eq)<br>=C[(R_1R_2)/(R_1+R_2)] :. alpha = (1/tau_c) = (R_1 + R_2)/(CR_1R_2).
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One or More

In given LR circuit the switch S is closed at time t=0 thenAThe ratio of induced emfs in the inductors of inductance L and 2L will be constantBThe ratio of induced emfs in the inductor of inductance L and 2L will be time varyingCthe potential difference VA−VB increases with timeDThe potential difference VA−VB will be constant - Question 2 - Select One
In given circuit, switch S is closed at t=0 . The charge on the capacitor ar steady state will be
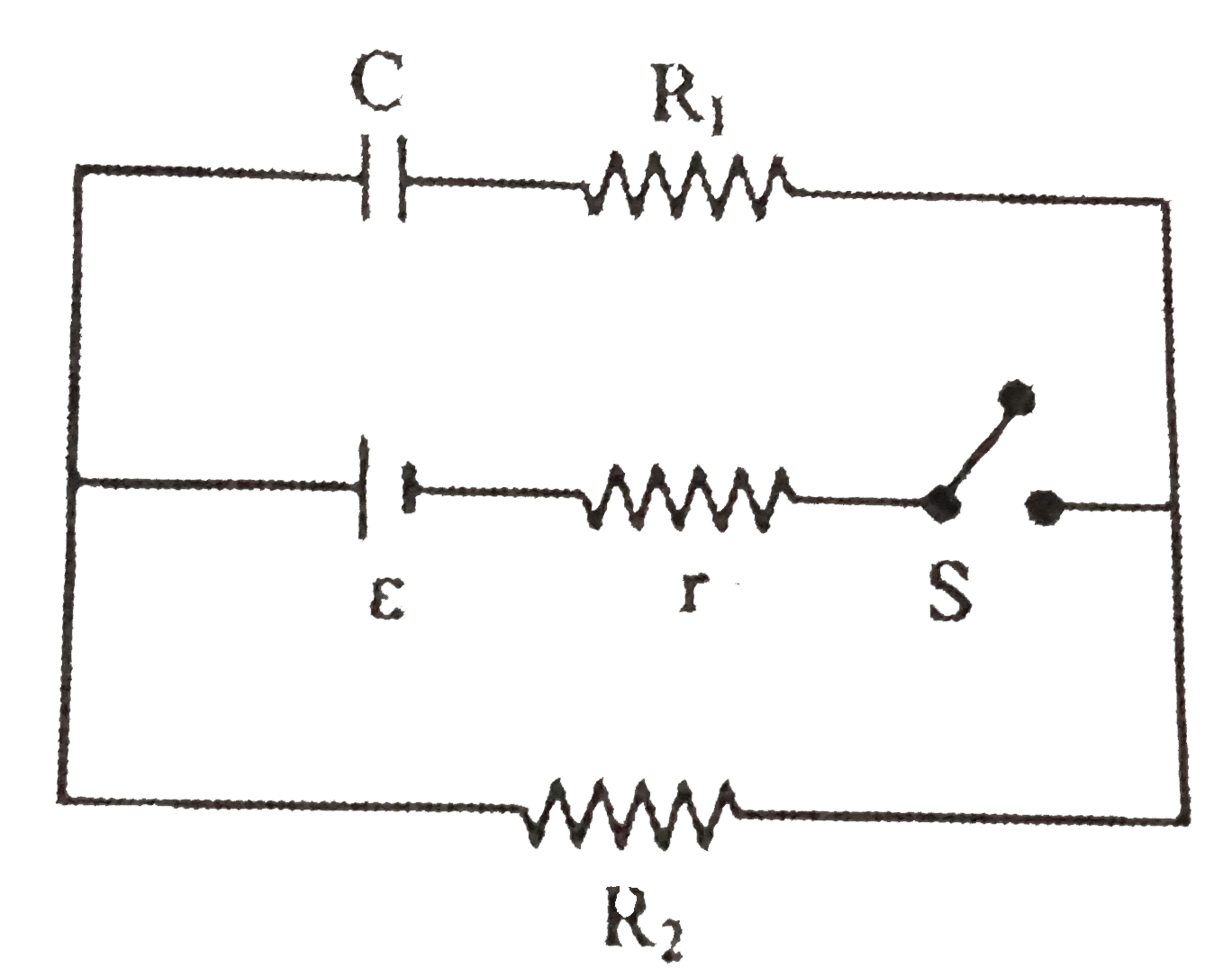 ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2
ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2 - Question 3 - Select One or More
In the given circuit Fig the switch is closed at t=0. Choose the correct answers.
 ACurrent in the inductor when the circuit reaches the steady state is 4A.BThe net change in flux in the inductor is 1.5Wb.CThe time constant of the circuit after closing S is 555.55sDThe charge stored in the capacitor in steady state is 1.2mC.
ACurrent in the inductor when the circuit reaches the steady state is 4A.BThe net change in flux in the inductor is 1.5Wb.CThe time constant of the circuit after closing S is 555.55sDThe charge stored in the capacitor in steady state is 1.2mC.
The switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
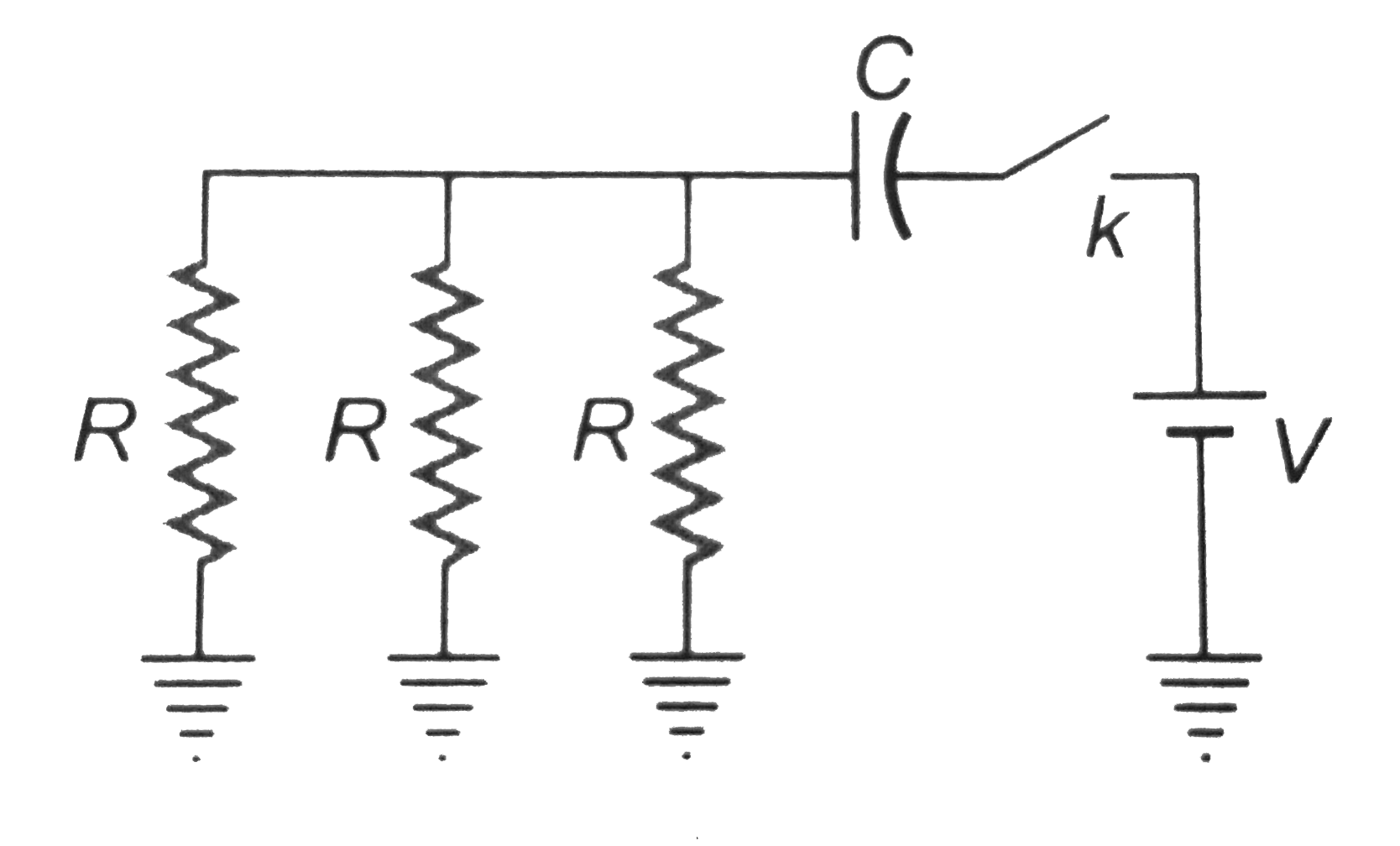 View Solution
View SolutionIn the given circuit switch is closed at t=0. The charge flown in time t=Tc (where Tc is time constant).
 View Solution
View SolutionIn the circuit shown in figure switch S is closed at time t=0

Current I from the battery at time t is given byView SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
 View Solution
View SolutionIn the given at t=0, switch S is closed.
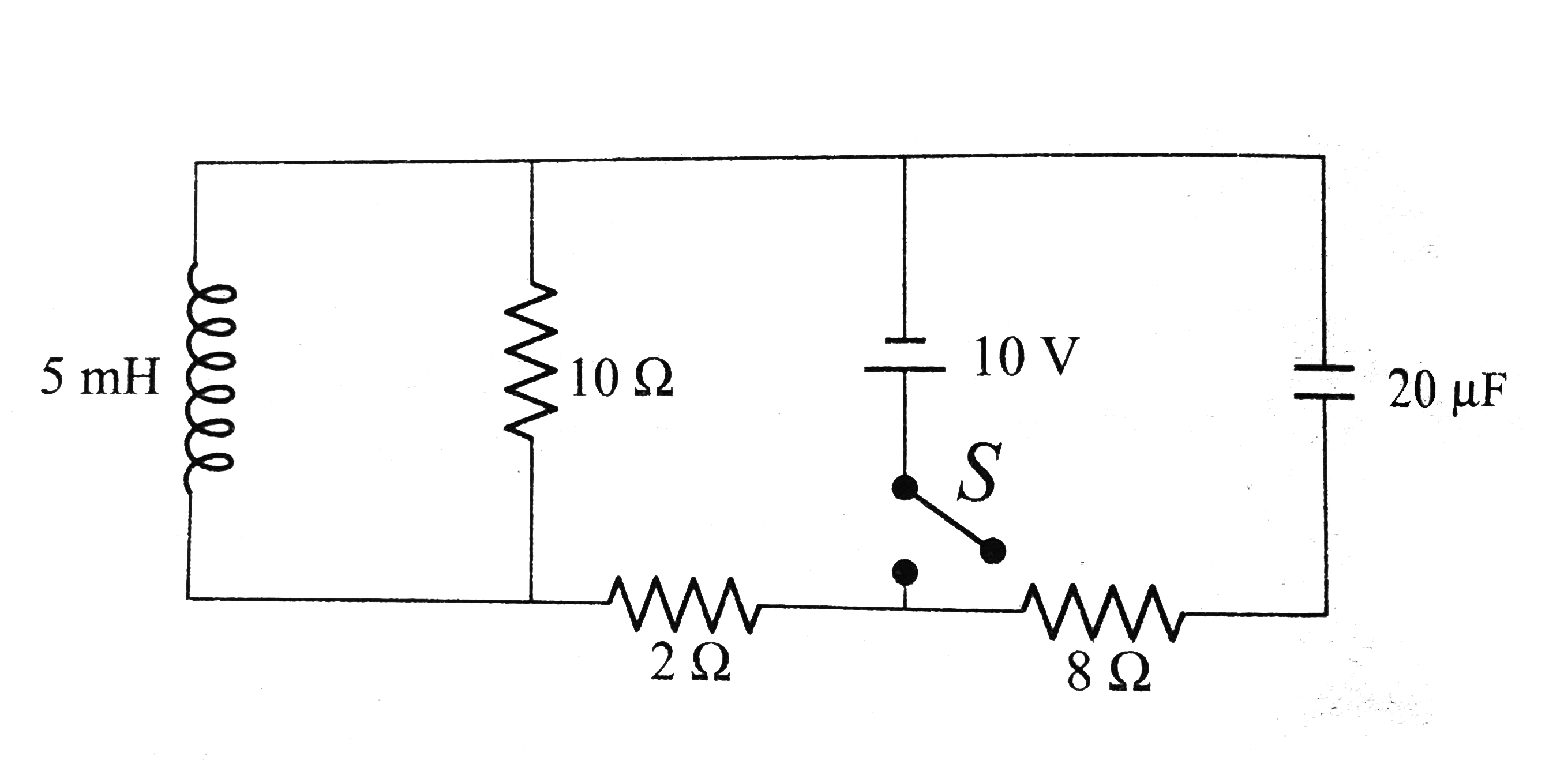
The energy stored in the inductor at any instant t(0<t∞) will beView Solution