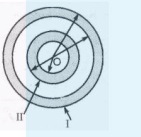
The inner and outer diameters of ring 1 of a dartboard are 32cm and 34cm respectively and those of rings II are 19cm and 21cm respectively. What is the total area of these two rings?

Video Solution

Text Solution

Verified by Experts

Given: For Ring I, $r_{1} = 16 and r_{2} = 17$
For Ring II, $r_{1} = 9.5 and r_{2} = 10.5$
Area of ring I = $(π \times 17^{2} - π \times 16^{2}) c m^{2}$
$= \frac{22}{7} \times (17^{2} - 16^{2}) c m^{2}$
$= \frac{22}{7} \times (17 + 16) (17 - 16) c m^{2}$
$= \frac{22}{7} \times 33 c m^{2}$
Area of ring II $= (π \times {10.5}^{2} - π \times {9.5}^{2}) c m^{2}$
$= π ({10.5}^{2} - {9.5}^{2}) c m^{2}$
$= \frac{22}{7} \times (10.5 - 9.5) (10.5 + 9.5) c m^{2}$
$= \frac{22}{7} \times 20 c m^{2}$
Total area of two ring $= \frac{22}{7} \times 33 + \frac{22}{7} \times 20 c m^{2}$
$= \frac{22}{7} \times (33 + 20) c m^{2}$
$= 166.57 c m^{2}$

Updated on:21/07/2023