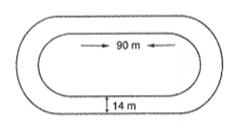
The inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If the track is everywhere 14m wide, find the area of the track. Also find the length of the outer running track.
The inside perimeter of the track =400 m
Width of the track =14 m
The total length of the two straight portions =90+90=180 m
Therefore, the length of the remaining portion (Semi-circular portions) =400−180=220 m
Circumference of the two remaining semi-circular portions = πr+πr=2πr
′r′ is the radius.
⇒2πr=220
⇒2×227×r=220
⇒44r=220×7
⇒r=35 m
So, the radius of the circular portion of the outer running running track =35m+14m=49 m
Area of the track =
[Area of the two rectangles of dimensions 90 m×14 m] + The area of the circular rings. [Two semi- circular rings will make a circle]
=2×90×14+227×(492−352)
=2520+227×(2401−1225)
=2520+22×11767
=6216m2
Length of the outer running track =2× length of straight track (i.e. 90 m) +2× Circumference of outer circle
=2×90+2×227×49
=180+308=488m
Length of the outer running track =488 m
Topper's Solved these Questions
Similar Questions
The inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If track is everywhere 14m wide, find the area of the track. Also, find the length of the outer running track.
View SolutionThe inner perimeter of a running track (shown in figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semicircular. If the track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

View Solution
Knowledge Check
The inside perimeter of a practice running track with semicircular ends and straight parallel sides is 312 m. The length of the straight portion of the track is 90 m. If the track has a uniform width of 2 m throughout, find its area.
 A5166 m2B5802.57 m2C636.57 m2D1273.14m2
A5166 m2B5802.57 m2C636.57 m2D1273.14m2The inner circumference of a circular race track 7 m wide is 440 m. Find the radius of the outer circle.
A57 mB68 mC77 mD69 mThe inner circumference of a circular race track, 14 m wide, is 440 m. Find the radius of the outer circle.
A70 mB56 mC77 mD84 m
The inside perimeter of a running track is 340m. The length of each straight portion is 60m and the curved portions are semicircles. If the trackis 7m wide, find the area of the track. Also, find the outer perimeter of the track.
View SolutionThe inside perimeter of a running track with semi circular ends and straight parallel sides is 888 metres. The length of the each of the straight portion of sides is 180 metre. If the track has an uniform width 2.10 metres throughout, find its area, also find its external perimeter.
View SolutionThe inner and outer radius of a circular track are 56 m and 63m respectively. Find the area of the track
View SolutionBajinder runs ten times around a square track and covers 4km. Find the length of the track.
View SolutionA running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides.
View Solution
