The internal bisectors of the angles of a ΔABC meet the sides BC, CA, AB in D,E and F, respectively. Show that the area of the ΔDEF is equal to,
2Δabc(b+c)(c+a)(a+b) Solution in Punjabi
The correct Answer is:Area of ΔDEF=2abcΔ(a+b)(b+c)(c+a)
Step by step video & image solution for The internal bisectors of the angles of a DeltaABC meet the sides BC, CA, AB in D,E and F, respectively. Show that the area of the DeltaDEF is equal to, (2Deltaabc)/((b+c)(c+a)(a+b)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
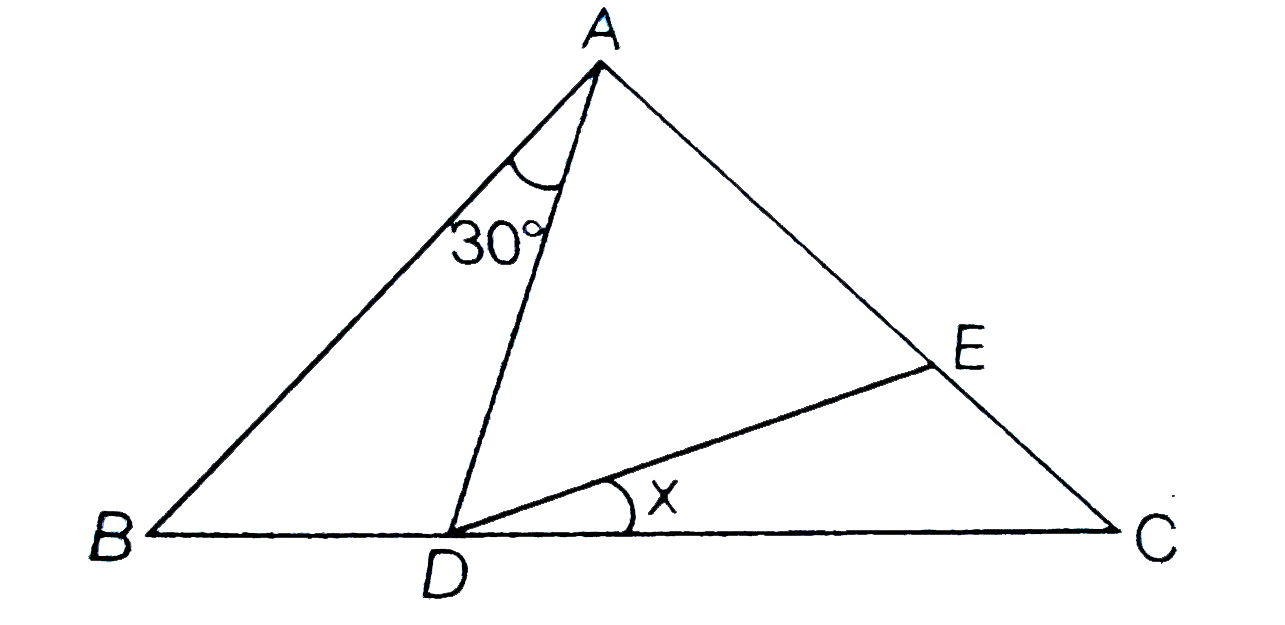
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionInternal bisector of /_A of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent sides of DeltaABC, then
View SolutionIn ΔABC, internal angle bisector of ∠A meet side BC in D. DE⊥AD meet AC in E and AB in F. then
View Solutionएक त्रिभुज ABC की भुजाओं AB,BC,CA के मध्य बिंदु क्रमशः D,E और F हैं। ΔDEF और ΔABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
View Solutionएक त्रिभुज ABC की भुजाओं AB,BC और CA के मध्य बिन्दु क्रमशः D,E और F हैं । ΔDEF और ΔABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए ।
View SolutionA(-1,5),B(3,1)and C(5,7) are the vertices of the ΔABC. If D ,E and F are the mid - points of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CAand¯¯¯¯¯¯AB respectively , find the area of ΔDEF. Show also that , ΔABC=4ΔDEF.
View SolutionD,E,F are midpoints of sides BC,CA,AB of ΔABC. Find the ratio of areas of ΔDEF and ΔABC.
View SolutionD,Eand F are respectively the mid - points of sides AB, BC and CA of ΔABC . Find the ratio of the areas of ΔDEFandΔABC.
View SolutionIn ΔABC and ΔDEF, AB= DE, AB || DE, BC= EF and BC|E|F. Vertices A, B and C are joined to vertices D, E and F respectively. Show that
ΔABC≅ΔDEF.
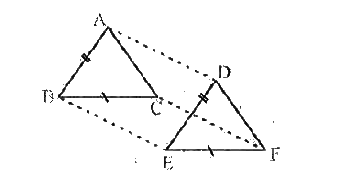
View SolutionThe coordinatea of A,B and C of the ΔABC are (3,1), (9,7) and (-3,7) respectively. If D,E and F are the mid-point of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CAand¯¯¯¯¯¯AB respectively, then find the area of the ΔDEF. Also show that ΔABC=4ΔDEF.
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View SolutionIn TriangleABC with fixed length of BC, the internal bisector of angle C meets the side ABatD and the circumcircle at E . The maximum value of CD×DE is c2 (b) c22 (c) c24 (d) none of these
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
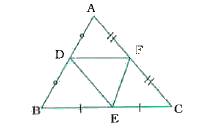
View Solution
