The length of DB is
12 m
16 m
6 m
3 m
The correct Answer is:B
Step by step video, text & image solution for The length of DB is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART - B (SECTION - III)8videos
SAMPLE PAPER 8
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART - B (SECTION - IV)12videos
SAMPLE PAPER 8
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART - A (SECTION - I)21videos
SAMPLE PAPER 8
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - V)8videos
SAMPLE PAPER 7
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9EXERCISE - SECTION C10videos
SAMPLE PAPER 9
Similar Questions
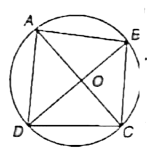
In the given figure ABCD is a cyclic quadrilateral DO=8cmandCO=4cm.AC is the angle bisector of ∠BAD. The length of AD is equal to the length of AB. DB intersects diagonal AC at O, then what is the length of the diagonal AC ?
 View Solution
View SolutionThe points C and D on a semicircle with AB as diameter are such that AC=1, CD=2, and DB=3. Then the length of AB lies in the interval
View Solution
Knowledge Check
- Question 1 - Select One
The area of the figure ABCEFGA is 84 m2. AH = HC = AG = 6 m and CE = HF = 4 m. If the angles marked in the figure are 90∘, then t he length of DB will be
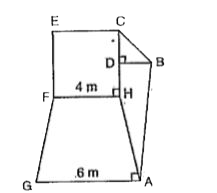 A2.5 mB5 mC6 mD12 m
A2.5 mB5 mC6 mD12 m - Question 2 - Select One
In ΔABC∠A=∠B=60∘,AC=√13cm. The lines ADandBDintersect at D with ∠D=90∘. If DB=2cm, then the length of AD is
A3 cmB3.5 cmC4 cmD4.7 cm - Question 3 - Select One
Two chords ABandPQ of a circle intersect at D inside a circle. If AD = 4 cm., DB = 6 cm., QD = 3 cm., the length of PQ is equal to
A11 cmB8 cmC9 cm.D10 cm.
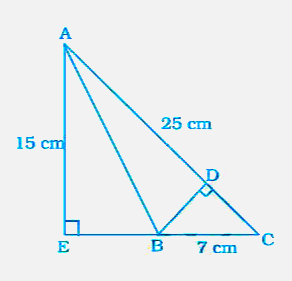
In Fig. 9.65, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.
 View Solution
View SolutionIn the figure ∠AED=∠ABC,AD=3,DB=5,AE=4 then length of AC is ..
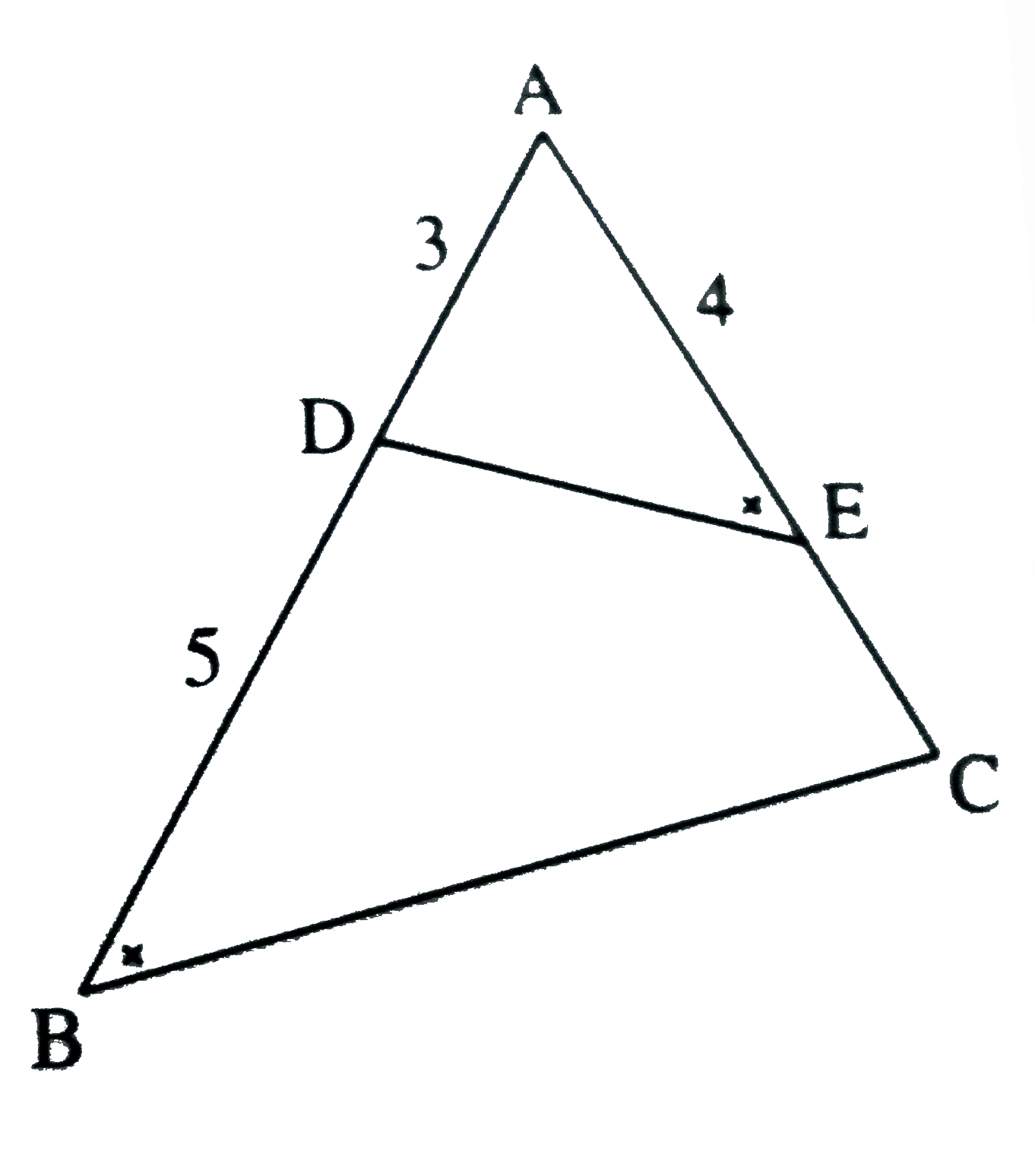 View Solution
View SolutionIf OA=→a;OB=→b;OC=2a+3b,OD=a−2b, the length of OA is three times the length of OB and OA is perpendicular to DB, then (BD×AC).(OD×OC) is
View SolutionPoints A, B and C are collinear. Point B is the mid-point of the line segment AC. Point D is not collinear with the other points. DA=DBandDB=BC=10. What is the length of DC?
View SolutionIn the equilateral triangle ABC given below, AD = DB and AE = EC. If I is the length of a side of the triangle, then what is the area of the shaded region ?
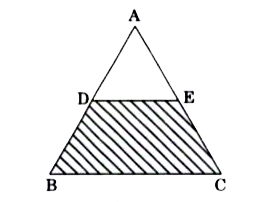 View Solution
View Solution

