Points A, B and C are collinear. Point B is the mid-point of the line segment AC. Point D is not collinear with the other points. DA=DBandDB=BC=10. What is the length of DC?
Step by step video & image solution for Points A, B and C are collinear. Point B is the mid-point of the line segment AC. Point D is not collinear with the other points. DA = DB and DB = BC = 10. What is the length of DC? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The mid - point of the line segment joining the points A(a,0) and B(0,b) is ………. .
View SolutionIf O be the origin the vector −−→OP is called the position vector of point P. Also −−→AB=−−→OB−−−→OA. Three points are said to be collinear if they lie on the same stasighat line.Points A,B,C are collinear if one of them divides the line segment joining the others two in some ratio. Also points A,B,C are collinear if and only if −−→AB×−−→AC=→0 Let the points A,B, and C having position vectors →a,→band→c be collinear Now answer the following queston: (A) →a.→b=→a.→c (B) →a×→b=→c (C) →a×→b+→b×→c+→c×→a=→0 (D) none of these
View Solution
Knowledge Check

In the figure, A, B, C and D are points on a line in the order. If AC = 5 , BD = 10 and AD = 13, then what is the length of BC ?A2B8C15D18
In ΔABC,D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC, If BC=12,what is the length of FG?A4B6C8D9If the points A(1, 2), B(2, 4) and C(3, a) are collinear, what is the length BC ?
A√2 unitB√3 unitC√5 unitD5 unit
If O be the origin the vector −−→OP is called the position vector of point P. Also −−→AB=−−→OB−−−→OA. Three points are said to be collinear if they lie on the same stasighat line.Points A,B,C are collinear if one of them divides the line segment joining the others two in some ratio. Also points A,B,C are collinear if and only if −−→AB×−−→AC=→0 Let the points A,B, and C having position vectors →a,→band→c be collinear Now answer the following queston: (A) veca.vecb=veca.vecc(B)vecaxxvecb=vecc(C)vecaxxvecb+vecbxxvecc+veccxxveca=vec0 (D) none of these
View SolutionIf the points A(1, 2), B(2, 4) and C(3, a) are collinear, what is the length BC ?
View Solution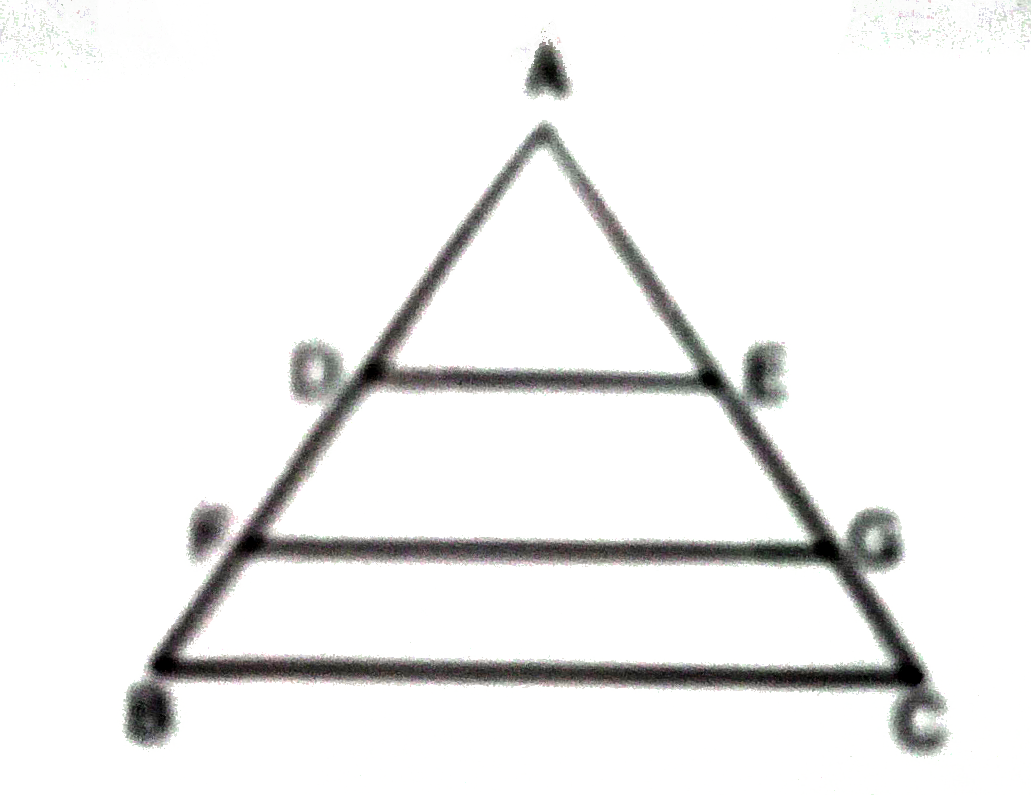 In ΔABC , D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC. What is the ratio of areas of FDEG and BFGC?
In ΔABC , D and E are the mid-points of AB and AC. Again, F and G are the mid-points of DB and EC. What is the ratio of areas of FDEG and BFGC?
View SolutionLet D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
View SolutionA and B are two points and C is any point collinear with A and B .If AB=10, BC =5, then AC is equal to :
View Solution
