The length of the common chord of the two circles $x^{2} + y^{2} - 4 y = 0$ and $x^{2} + y^{2} - 8 x - 4 y + 11 = 0$ is

A

$\frac{\sqrt{145}}{4}$ cm

B

$\frac{\sqrt{11}}{2} c m$

C

$\sqrt{135}$ cm

D

$\frac{\sqrt{135}}{4} c m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given , equation of cirlcesare
$x^{2} + y^{2} - 4 y = 0$
and $x^{2} + y^{2} - 8 x - 4 y + 11 = 0$
$∴$ Equation of chord is
$x^{2} + y^{2} - 4 y - (x^{2} + y^{2} - 8 x - 4 y + 11) = 0$
$\Rightarrow 8 x 11 = 0$

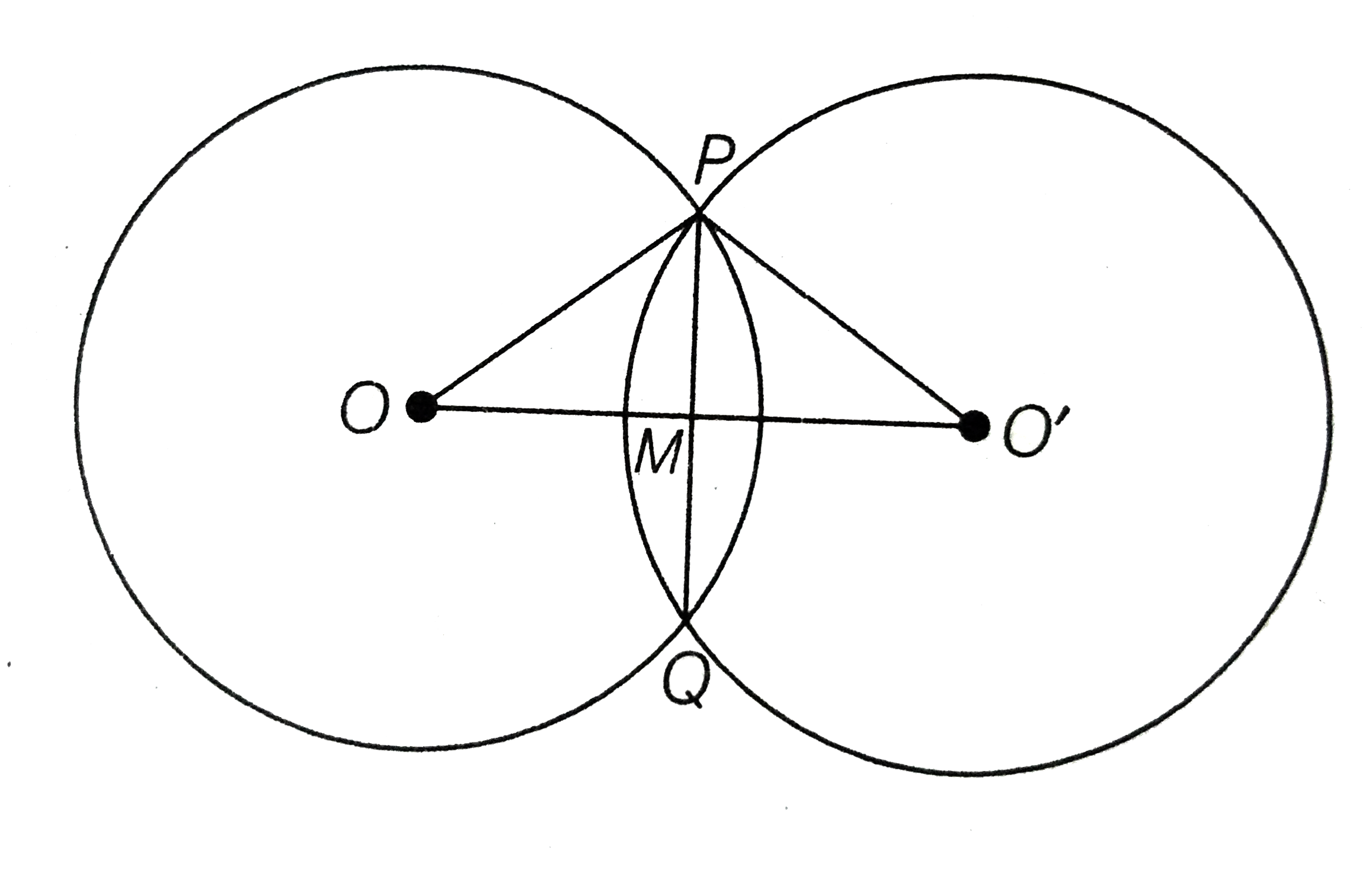
So , centre and radius of first circle are O(0,2) and OP = r= 2.
Now , perpendicular distance form O(0,2) to the line 8x - 11 is
$d = O M = \frac{| 8 \times 0 - 11 |}{\sqrt{8^{2}}} = \frac{11}{8}$
In $Δ O M P, P M = \sqrt{O P^{2} - O M^{2}}$
$= \sqrt{2^{2} - {(\frac{11}{8})}^{2}} = \sqrt{4 - \frac{121}{64}}$
$= \frac{\sqrt{256 - 121}}{64} = \frac{\sqrt{135}}{4} c m$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The length of the common chord of the two circle $x^{2} + y^{2} - 4 y = 0$ and $x^{2} + y^{2} - 8 x - 4 y + 11 = 0$ is
A $\frac{\sqrt{145}}{4}$ cm
B $\frac{\sqrt{11}}{2}$ cm
C $\sqrt{135}$ cm
D $\frac{\sqrt{135}}{4}$ cm
Question 2 - Select One
The length of the common chord of the circles $x^{2} + y^{2} - 2 x - 1 = 0$ and $x^{2} + y^{2} + 4 y - 1 = 0$ , is
A $\sqrt{15 / 2}$
B $\sqrt{15}$
C $2 \sqrt{15}$
Dnone of these
Question 3 - Select One
The length of the common chord of the circles $x^{2} + y^{2} + 2 x + 3 y + 1 = 0$ and $x^{2} + y^{2} + 4 x + 3 y + 2 = 0$ is
A $\frac{9}{2}$
B $2 \sqrt{2}$
C $3 \sqrt{2}$
D $\frac{3}{2}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 11 -PAPER 2 (MATHEMATICS )

Home
Ask Doubt
Profile