The length of the transversal common tangent to the circle $x^{2} + y^{2} = 1$ and ${(x - t)}^{2} + y^{2} = 1$ is $\sqrt{21}$ , then t=

A

$\pm 2$

B

$\pm 5$

C

$\pm 3$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

If d is the distance between the centres of two circles of radii $r_{1}$ and $r_{2}$ , then
Length of transversal common tangent $= \sqrt{d^{2} - {(r_{1} + r_{2})}_{1}^{2}}$

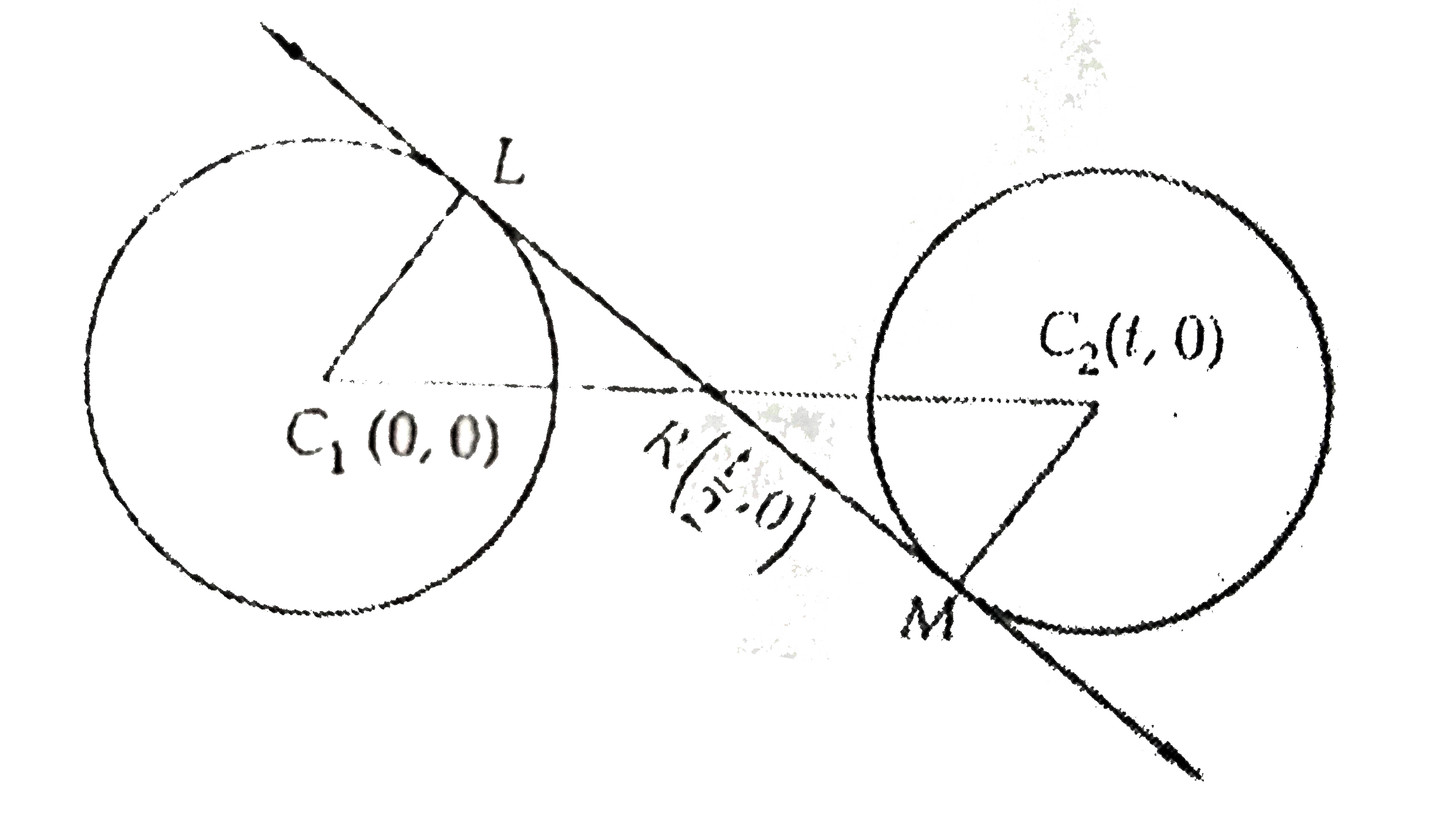
Centres of the given circles are $C_{1} (0, 0)$ and $C_{2} (t, 0)$ and corresponding radii are $r_{1} = 1$ and $r_{2} = 1$ respectively.
$∴ d = \sqrt{{(t - 0)}^{2} + 0} = | t |$
It is given that :
Length of transversal common tangent $= \sqrt{21}$
$\Rightarrow \sqrt{d^{2} - {(r_{1} + r_{2})}_{1}^{2}} = \sqrt{21} \Rightarrow t^{2} - 2^{2} = 21 \Rightarrow t = \pm 5$
$ALITER - -------- -$ Since given circles are of equal radius. Therefore, R is the mid-point of $C_{1} C_{2}$ . Also , $Δ C_{1} L R ≅ Δ C_{2} M R$ .
$∴$ R is the mid-point of LM.
In $Δ C_{1} L R$ , we have
$C_{1} R^{2} = C_{1} L^{2} + L R^{2}$
$\Rightarrow L R = \sqrt{C_{1} R^{2} - C_{1} L^{2}} = \sqrt{\frac{t^{2}}{4} - 1} = \sqrt{\frac{t^{2} - 4}{2}}$
$∴ L M = \sqrt{21}$
$\Rightarrow 2 L R = \sqrt{21} \Rightarrow \sqrt{t^{2} - 4} = \sqrt{21} \Rightarrow t^{2} = 25 \Rightarrow t = \pm 5$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A common tangent to the circles $x^{2} + y^{2} = 4$ and ${(x - 3)}^{2} + y^{2} = 1$ , is
Ax=4
By=2
C $x + \sqrt{3} y = 4$
D $x + 2 \sqrt{2} y = 6$
Question 2 - Select One
The number of common tangents of the circles $x^{2} + y^{2} = 16$ and $x^{2} + y^{2} - 2 y = 0$ is $:$
A2
B3
C4
D0
Question 3 - Select One
The number of common tangents to the circles $x^{2} + y^{2} - y = 0 and x^{2} + y^{2} + y = 0$ is
A2
B3
C0
D1

OBJECTIVE RD SHARMA-CIRCLES-Chapter Test

Home
Ask Doubt
Profile