Question

The length of two parallel chords of a circle are 6 cm and 8 cm . The radius of the circle is 5 cm. Find the distance btween them if :
(i) chords are on the same side of the centre.
(ii) chords are on the opposite side of the centre.

Answer

(i) 1 cm
(ii) 7 cm

Explanation

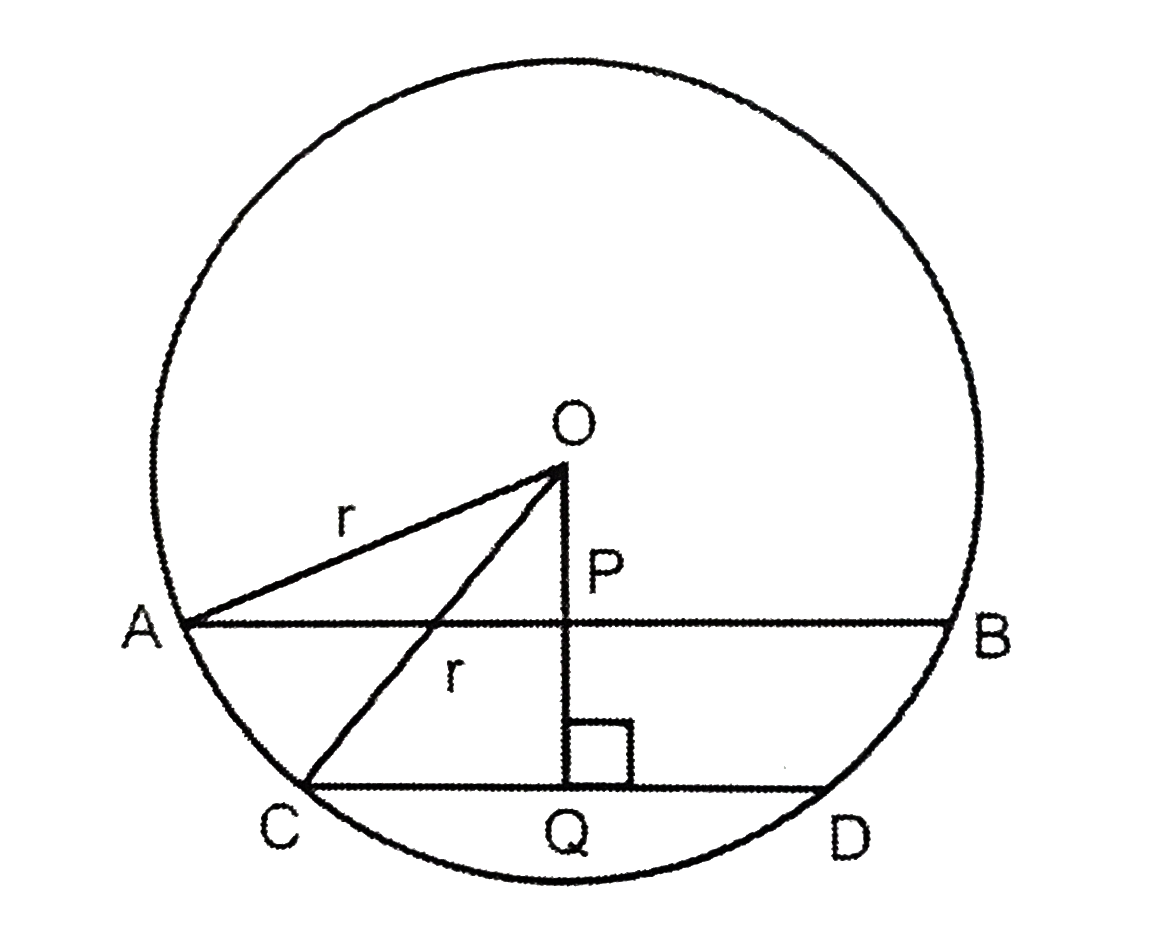
To solve the problem, we need to find the distance between two parallel chords of a circle given their lengths and the radius of the circle. We will solve the problem for both cases: when the chords are on the same side of the center and when they are on opposite sides.

Given:
- Length of chord AB = 6 cm
- Length of chord CD = 8 cm
- Radius of the circle (r) = 5 cm

Step 1: Find the distances from the center to each chord.

1. For chord AB:
- The length of chord AB is 6 cm. Therefore, half of this length is:
\( AM = MB = \frac{6}{2} = 3 \text{ cm} \)
- Let ON be the perpendicular distance from the center O to chord AB. Using the Pythagorean theorem in triangle OMB:
\( OB^2 = OM^2 + MB^2 \)
Substituting the known values:
\( 5^2 = OM^2 + 3^2 \)
\( 25 = OM^2 + 9 \)
\( OM^2 = 25 - 9 = 16 \)
\( OM = 4 \text{ cm} \)

2. For chord CD:
- The length of chord CD is 8 cm. Therefore, half of this length is:
\( CN = ND = \frac{8}{2} = 4 \text{ cm} \)
- Let ON be the perpendicular distance from the center O to chord CD. Using the Pythagorean theorem in triangle ONC:
\( OC^2 = ON^2 + NC^2 \)
Substituting the known values:
\( 5^2 = ON^2 + 4^2 \)
\( 25 = ON^2 + 16 \)
\( ON^2 = 25 - 16 = 9 \)
\( ON = 3 \text{ cm} \)

Step 2: Calculate the distance between the chords.

1. If the chords are on the same side of the center:
- The distance NM between the chords is given by:
\( NM = OM - ON = 4 - 3 = 1 \text{ cm} \)

2. If the chords are on opposite sides of the center:
- The distance NM between the chords is given by:
\( NM = OM + ON = 4 + 3 = 7 \text{ cm} \)

Final Answers:
- (i) Distance between the chords when they are on the same side = 1 cm
- (ii) Distance between the chords when they are on opposite sides = 7 cm