The line L1≡4x+3y−12=0 intersects the x-and y-axies at AandB, respectively. A variable line perpendicular to L1 intersects the x- and the y-axis at P and Q , respectively. Then the locus of the circumcenter of triangle ABQ is 3x−4y+2=0 4x+3y+7=0 6x−8y+7=0 (d) none of these
3x-4y+2 = 0
4x+3y+7 = 0
6x-8y+7=0
none of these
The correct Answer is:C
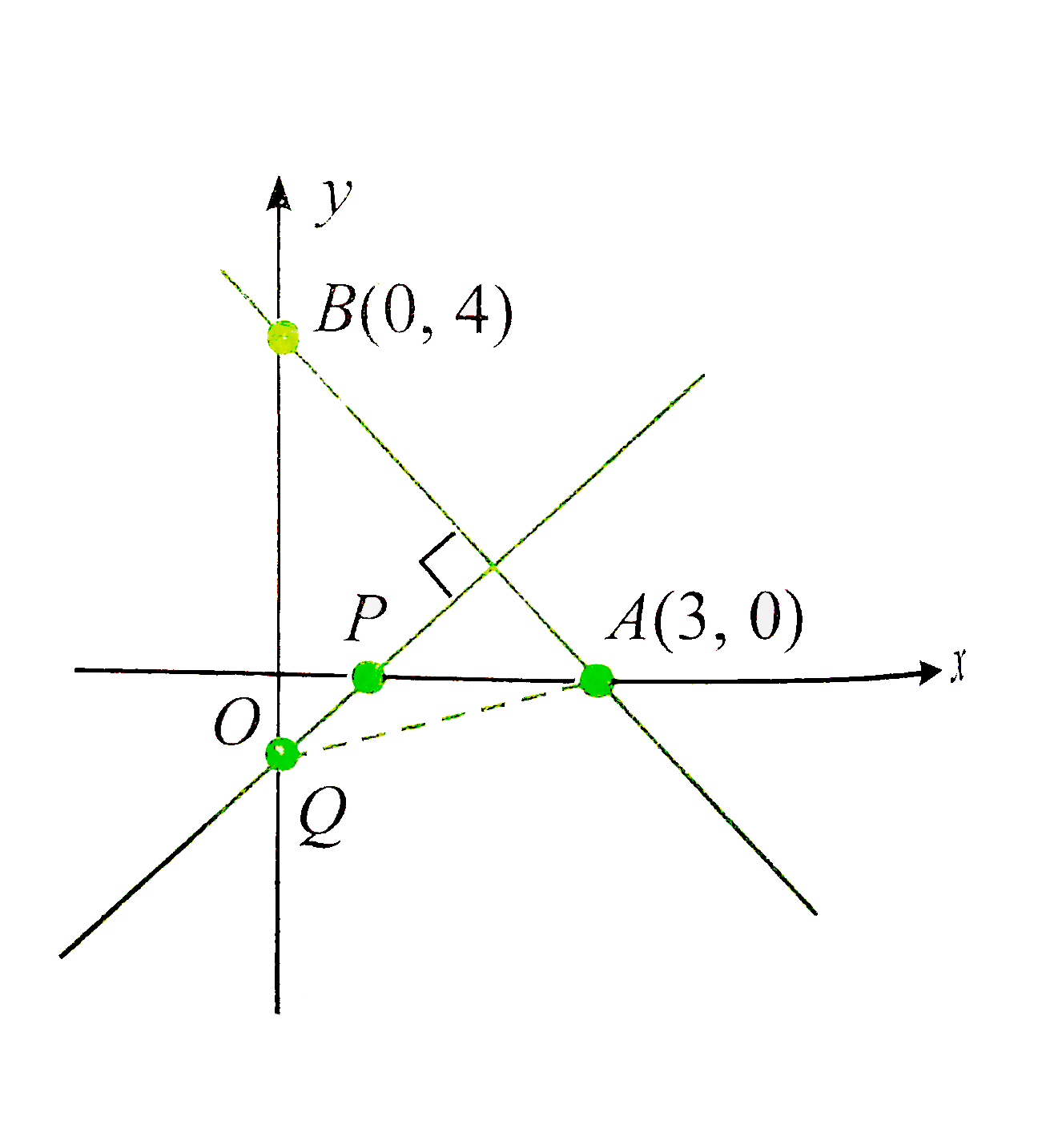
Clearly, the circumcenter of triangle ABQ will lie on the perpendicular bisector of line AB. Now, the equation of perpendicular bisector of line AB is 3x-4y+7/2=0. Hence, the locus of circumcenter is 6x-8y+7=0.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)30videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
The line L1≡4x+3y−12=0 intersects the x-and y-axies at A and B, respectively. A variable line perpendicular to L1 intersects the x- and the y-axis at P and Q , respectively. Then the locus of the circumcenter of triangle ABQ is (a) 3x−4y+2=0 (b) 4x+3y+7=0 (c) 6x−8y+7=0 (d) none of these
View SolutionLet a line L1:3x+2y−6=0 intersect the x and y axes at P and Q respectively. Let another line L2 perpendicular to L1 cut the x and y axes at R and S respectively.The locus of point of intersection of the lines PS and QR is
View Solution
Knowledge Check
- Question 1 - Select One
The line 3x + 4y - 24 = 0 intersects the X - axis at A and Y-axis at B . Then the Circumcentre of the ΔOAB , where O is the origin is
A(2 , 3)B(3 , 3)C(4 ,3 )DNone of these
A line intersects x-axis at A(7,0) and y-axis at B(0,-5). A variable line PQ which is perpendicular to AB intersects x -axis at P and y -axis at Q. If AQ and BP intersect at r then locus of R is ………
View SolutionA line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. Image of the locus of R in the line y=−x is : (A) x2+y2−2x+4y=0 (B) x2+y2+2x+4y=0 (C) x2+y2−4y=0 (D) x2+y2+2x−4y=0
View SolutionA line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. The locus of R and the circle x2+y2−8y−4=0 (A) touch each other internally (B) touche the given circle externally (C) intersect in two distinct points (D) neither intersect nor touch each other
View SolutionThe coordinates of the point of intersection of the lines 3x+4y−18=0 and 4x−5y+7=0 are
View SolutionFrom a pointP=(3,4) perpendiculars PQ and PR are drawn to line 3x+4y−7=0 and a variable line y−1=m(x−7) respectively then maximum area of triangle PQR is :
View SolutionA line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. Locus of R is : (A) x2+y2−2x+4y=0 (B) x2+y2+2x+4y=0 (C) x2+y2−2x−4y=0 (D) x2+y2+2x−4y=0
View SolutionIf normal of circle x2+y2+6x+8y+9=0 intersect the parabola y2=4x at PandQ then find the locus of point of intersection of tangent's at PandQ.
View Solution

