Question

The line x+2y=1 cuts the ellipse ${\displaystyle x^2+4y^2=1}$ 1 at two distinct points A and B. Point C is on the ellipse such that area of triangle ABC is maximum, then find point C.

Answer

`(-(1)/(sqrt(2)),-(1)/(2sqrt(2)))`

Explanation

`(9x^(2))/(4)+3y^(2)=1` , which is required locus.

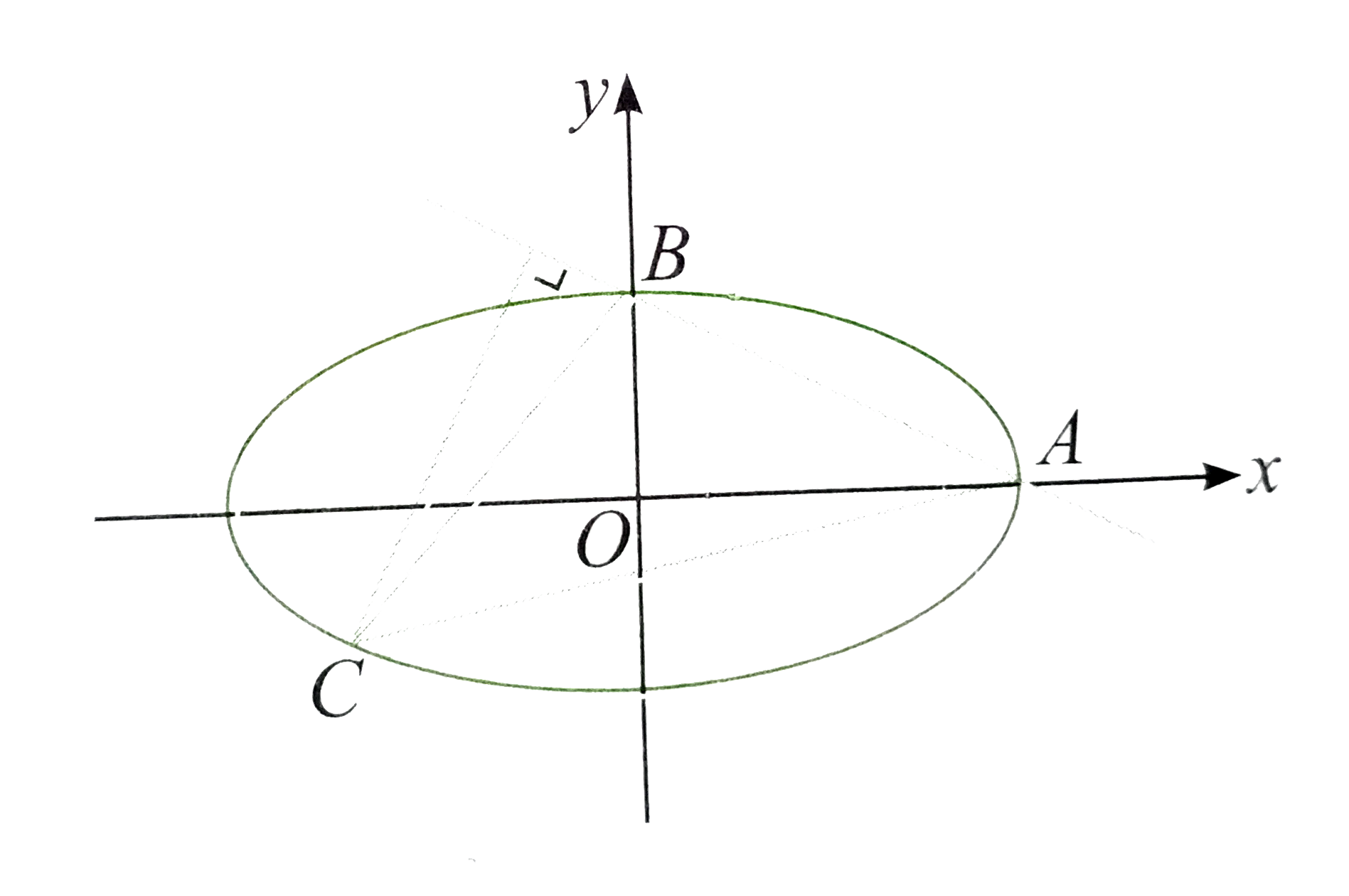
Clearly, line x+2y=1 cuts the ellipse `(x^(2))/(1)+(y^(2))/(1//4)=1` at `A(1,0) and B(0,2)`.
Let point C on the ellipse be `(cos theta, (sin theta)//2)`
Now, are of the triangle ABC is maximum, if distance of C from AB is maxiumm
Distance of C from AB, `d=|(cos theta+sin theta-1)/(sqrt(5))|`
Maximum value of d occur when `cos theta= sin theta=-(1)/(sqrt(2))`
`:. C-=(-(1)/(sqrt(2)),-(1)/(2sqrt(2)))`