The linear function y=g(x) is graphed in the xy-plane. IF g(-3)=4 and g(2)=19, what is the slope of line g?
The correct Answer is:3
To find the slope of the linear function g(x), we can use the formula for the slope between two points on a line. The slope m is calculated as follows:
Step 1: Identify the points
We are given two points based on the function values:
- Point 1: (−3,4) where g(−3)=4
- Point 2: (2,19) where g(2)=19
Step 2: Use the slope formula
The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
In our case:
- x1=−3, y1=4
- x2=2, y2=19
Step 3: Substitute the values into the formula
Substituting the values into the slope formula:
m=19−42−(−3)
Step 4: Simplify the numerator and denominator
Calculating the numerator:
19−4=15
Calculating the denominator:
2−(−3)=2+3=5
Step 5: Calculate the slope
Now substituting back into the slope formula:
m=155=3
Conclusion
The slope of the line g is 3.
---
We are given two points based on the function values:
- Point 1: (−3,4) where g(−3)=4
- Point 2: (2,19) where g(2)=19
The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
In our case:
- x1=−3, y1=4
- x2=2, y2=19
Substituting the values into the slope formula:
m=19−42−(−3)
Calculating the numerator:
19−4=15
Calculating the denominator:
2−(−3)=2+3=5
Now substituting back into the slope formula:
m=155=3
The slope of the line g is 3.
Topper's Solved these Questions
Similar Questions
If g(x)=x3−ax4, and g(2)=12 , what is the value of g(4)?
View Solution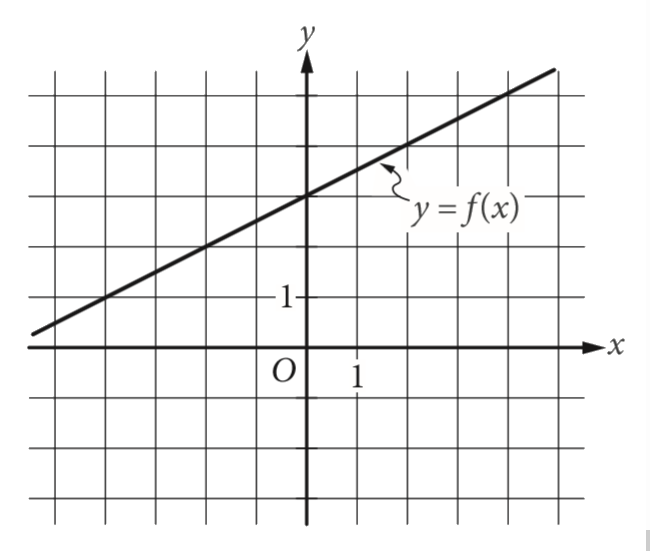
The graph of the linear functions f is shown in the xy-plane above. The slope of the graph of the linear function g is 4 times the slope of the graph of f. IF the graph of g passes through the point (0,-4) what is the value of g(9)?
View Solution
Knowledge Check

The figure above shows the graph of the linear function, y=f(x). If slope of the line is -2 and f(3)=4, what is the value of b?A8B9C10D11If function g is defined by g(x)=x-1 and 2g(c)=10, what is the value of g(3c)?
A6B9C15D17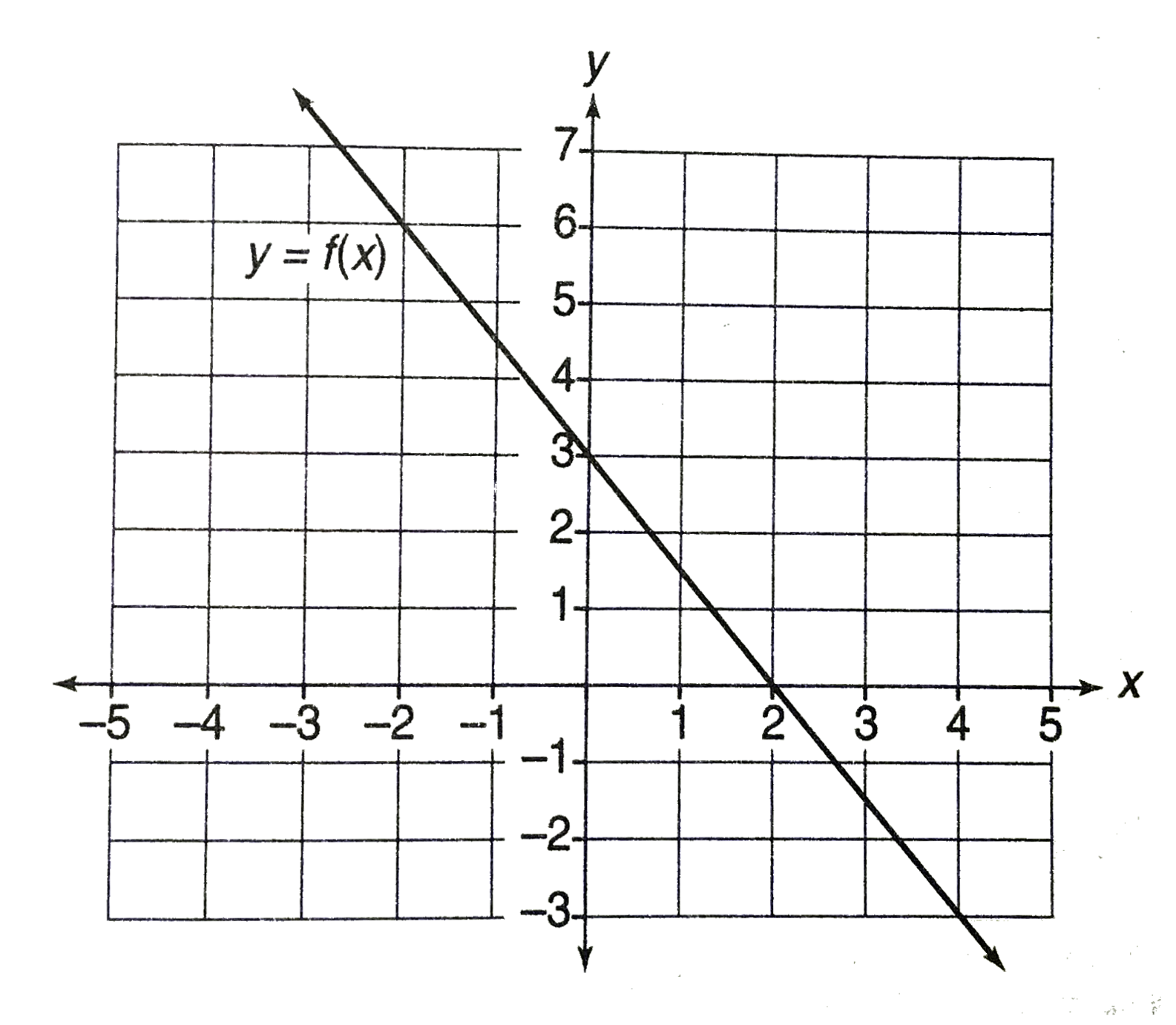
A linear function f is shown in the accompanying figure. If function g in the reflection of function f in the x-axis (not shown), what is the slope of the graph of function g?A−32B−23C23D32
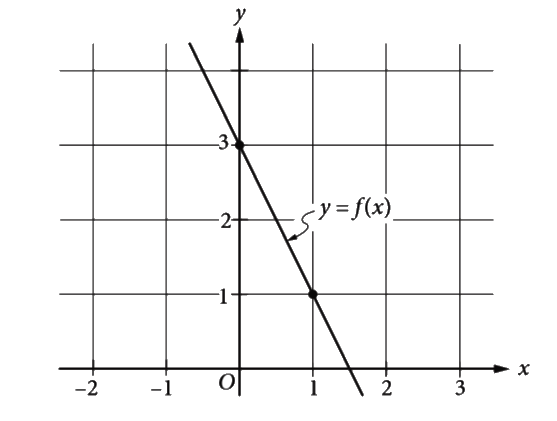
The graph of the linear function f is shown in the xy-plane above. The graph of the linear function g (not shown) is perpendicular to the graph of f and passes through the point (1,3). What is the value of g(0) ?
View SolutionIf g(x)=a√a(1−x) Function g is defined by the equation above. If g(−8)=375, what is the value of a?
View SolutionThe function g is defined above. What is the value of g(−4x) ?
View SolutionA function g(x) is defined as g(x)=−5x2. What is g(−2)?
View SolutionLet the function g be defined by g(x)=5x+2. If √g(a2)=6, what is the value of a?
View Solution
