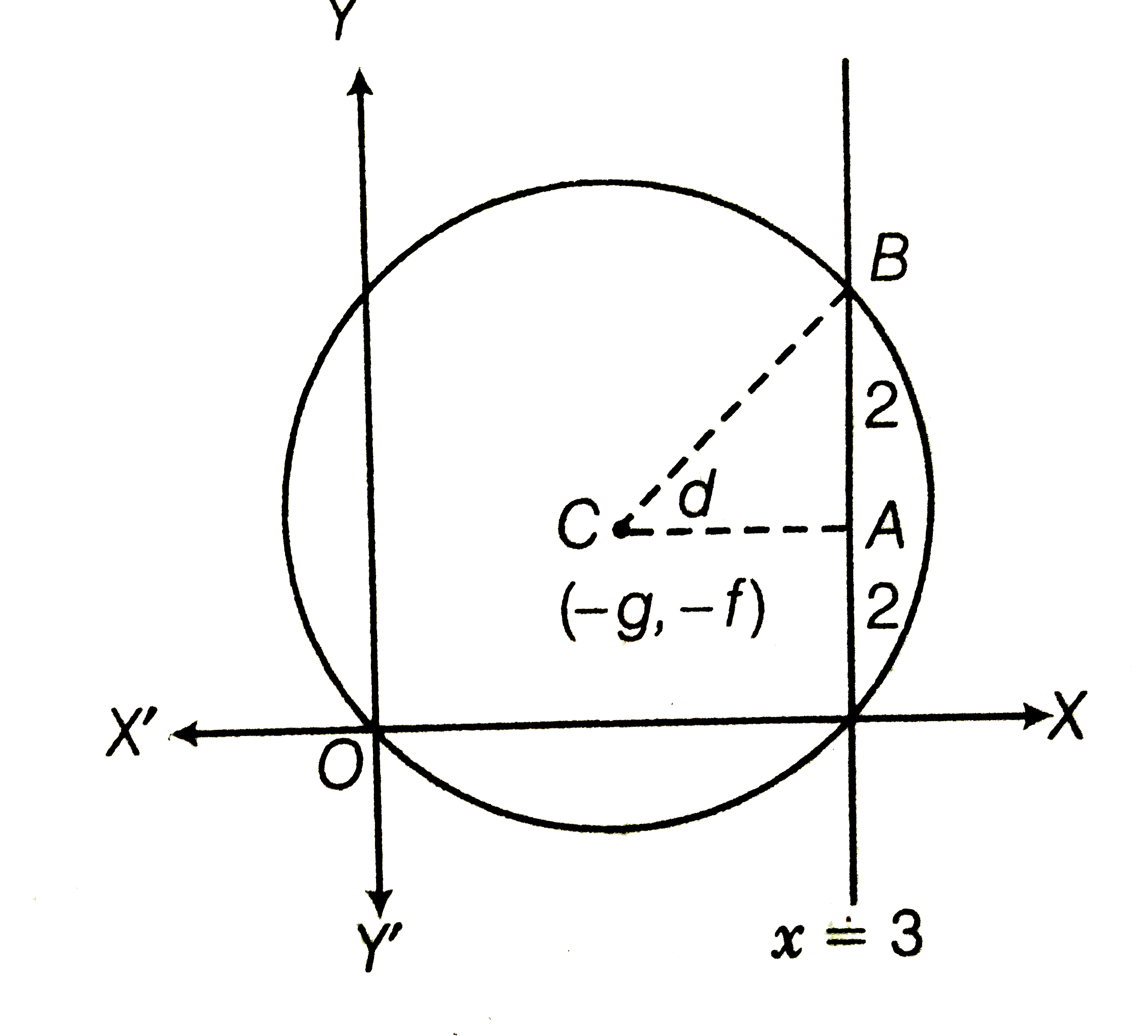
The locus of centre of a circle which passes through the origin and cuts off a length of 4 units on the line $x = 3$ is

A

$y^{2} + 6 x = 0$

B

$y^{2} + 6 x = 13$

C

$y^{2} + 6 x = 10$

D

$x^{2} + 6 y = 13$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let centre of circle be C(-g,-f), then equation of circle passing through origin is $x^{2} + y^{2} + 2 g x + 2 f y = 0$
$D i s tan c e, d$ d=|3-(-g)|=g+3 in DeltaABC,(bc)^(2)=Ac ^(2) +BA^(2) $< b r >$ rArr g^(2)+f^(2)=(g+3)^(2)+2^(2) $< b r >$ rArr g^(2)+f^(2)=g^(2)+6g+9+4 $< b r >$ therefore f^(2)=6g+13 $h e n c e, r e q u a t i o n l o c u s i s$ y^(2)+6x=13.

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE AND CONICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The locus of the centere of a circle which passes through the point (0,0) and cuts off a length 2b from the line x=c is-
A $y^{2} + 2 c x = b^{2} + c^{2}$
B $x^{2} + c x = b^{2} + c^{2}$
C $y^{2} + 2 c y = b^{2} + c^{2}$
Dnone of these
Question 2 - Select One
Equation of the circle which passes through the origin and cuts off intercepts of length 2 units from negative co-ordinate axes , is
A $x^{2} + y^{2} + 2 x + 2 y = 0$
B $x^{2} + y^{2} + 2 x - 2 y = 0$
C $x^{2} + y^{2} + 2 x + 2 y = 0$
D $x^{2} + y^{2} - 2 x - 2 y = 0$
Question 3 - Select One
Equation to the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is
A ${(x - 3)}^{2} + {(y - 2 \sqrt{3})}^{2} = {(3 \sqrt{2})}^{2}$
B ${(x - 2)}^{2} + {(y - 3 - 3 \sqrt{2})}^{2} = {(3 \sqrt{2})}^{2}$
C ${(x - 2 \sqrt{3})}^{2} + {(y - 3)}^{2} = {(3 \sqrt{2})}^{2}$
Dnone of these

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-CIRCLE AND CONICS-All Questions

Home
Ask Doubt
Profile