The locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
To find the locus of points inside a circle that are equidistant from two fixed points on the circumference of the circle, we can follow these steps:
1. Identify the Circle and Points:
Let’s denote the circle as O with radius r. Let the two fixed points on the circumference of the circle be A and B.
2. Draw the Circle:
Draw a circle with center O and radius r. Mark the points A and B on the circumference.
3. Join the Points A and B:
Draw a line segment connecting points A and B. This line segment represents the distance between the two fixed points.
4. Find the Midpoint:
Determine the midpoint M of the line segment AB. The coordinates of M can be found using the midpoint formula:
M=(xA+xB2,yA+yB2)
5. Draw the Perpendicular Bisector:
Construct the perpendicular bisector of the line segment AB. This line will pass through the midpoint M and will be perpendicular to AB.
6. Identify the Locus:
The locus of points that are equidistant from points A and B will be the line segment of the perpendicular bisector that lies inside the circle. This line segment represents all points that are equidistant from A and B.
7. Conclusion:
The locus of points inside the circle that are equidistant from the two fixed points A and B is the segment of the perpendicular bisector of AB that lies within the circle.
Let’s denote the circle as O with radius r. Let the two fixed points on the circumference of the circle be A and B.
Draw a circle with center O and radius r. Mark the points A and B on the circumference.
Draw a line segment connecting points A and B. This line segment represents the distance between the two fixed points.
Determine the midpoint M of the line segment AB. The coordinates of M can be found using the midpoint formula:
M=(xA+xB2,yA+yB2)
Construct the perpendicular bisector of the line segment AB. This line will pass through the midpoint M and will be perpendicular to AB.
The locus of points that are equidistant from points A and B will be the line segment of the perpendicular bisector that lies inside the circle. This line segment represents all points that are equidistant from A and B.
The locus of points inside the circle that are equidistant from the two fixed points A and B is the segment of the perpendicular bisector of AB that lies within the circle.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(A)26videos
LOCI (LOCUS AND ITS CONSTRUCTIONS)
- BOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions15videos
LINEAR INEQUATIONS
- BOOK - ICSECHAPTER - MATHEMATICS -2014EXERCISE - SECTION- B29videos
MATHEMATICS -2014
Similar Questions
Describe :
The locus of points within a circle that are equidistant from the end points of a given chord.View SolutionThe locus of the centres of all circles passing through two fixed points.
View SolutionA point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is
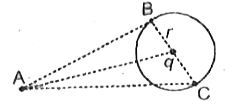
View SolutionA point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
 View Solution
View SolutionStatement-1: The locus of point z satisfying ∣∣∣3z+i2z+3+4i∣∣∣=32 is a straight line.
Statement-2 : The locus of a point equidistant from two fixed points is a straight line representing the perpendicular bisector of the segment joining the given points.View SolutionFind the equation of the circle in which the chord joining the points (a,b)and(b,−a) subtends an angle of 45∘ at any point on the circumference of the circle.
View SolutionThe locus of the mid-points of the chords of the circle of lines radiùs r which subtend an angle π4 at any point on the circumference of the circle is a concentric circle with radius equal to (a) r2 (b) 2r3 (c) r√2 (d) r√3
View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are
 View Solution
View SolutionThe locus of a point equidistant from two points with position vectors →a and →b is
View SolutionThe radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
View Solution
